循环神经网络入门

8.1 循环神经网络入门

探索循环神经网络的基础概念，使用 NumPy 从头实现情绪分析模型！

创建日期: 2025-01-18

循环神经网络 (Recurrent Neural Network, RNN) 是一种专门处理序列的神经网络，由于其在文本处理方面非常有效，因此常用于 自然语言处理 (Natural Language Processing, NLP) 任务中。本节我们将探索 RNN 是什么，理解其工作原理，并使用 Python 语言从头开始构建一个真正的 RNN 网络（仅使用 NumPy 库）。

这需要我们有神经网络的基础知识，如果不了解神经网络的概念，可以查看第 02 章深度学习原理和第 04 章详解反向传播算法的内容，让我们开始吧！

8.1.1 为什么

序列数据 (Sequence Data) 是指具有顺序性的结构化数据，通常以特定的时间或逻辑顺序排列。它在自然语言处理、时间序列分析、信号处理等领域中广泛使用。以下是序列数据的特点：

1. 顺序性

数据点之间的顺序至关重要，打乱顺序可能会丢失信息或改变数据的意义。比如股票价格：100, 102, 105, 101 ，顺序决定价格变化的趋势；句子中单词的顺序：“I am happy” 和 “Happy am I” 的意思不同。
2. 依赖性

前后数据点之间可能存在依赖关系，比如当前数据点只依赖于临近的点，或者当前数据依赖较远的历史数据。文本序列 “The cat is on the …” ，预测最后一个单词，通常只需要考虑最近的几个单词 “is on the” 。

序列数据具有独特的顺序性和依赖性，能够有效地表示时间、空间或逻辑顺序关系。在实际应用中，了解序列数据的特点并选择合适的分析方法和模型，对于提高预测精度和决策质量具有重要意义。

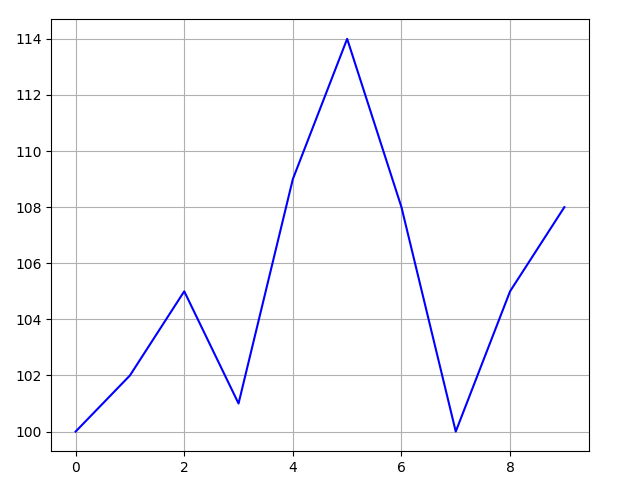
文件 1_1_sequence_data.py 对序列数据进行绘制（可以使用 yfinance 获取真实股票数据）：

stock = [100, 102, 105, 101, 109, 114, 108, 100, 105, 108]
pyplot.plot(range(len(stock)), stock, color='b')

结果如下图所示：

基础神经网络（包括 CNN ）的一个问题是它们只能处理预定大小的样本：使用固定大小的输入，并产生固定大小的输出。RNN 很有用，因为它们允许我们将可变长度的序列作为输入和输出。下图列举 RNN 的几种样式：

注：红色表示输入，绿色表示 RNN 自己，蓝色表示输出。

这种处理序列的能力使得 RNN 非常有用，以下是几个例子：

机器翻译（例如谷歌翻译）是通过“多对多” RNN 完成的，原始文本序列输入到 RNN 中，然后 RNN 生成翻译文本作为输出。
情绪分析模型通常使用“多对一” 的 RNN 网络。要分析的文本被输入到 RNN 中，然后 RNN 产生单个输出分类（正向或者负向）。

接下来，我们将从头构建一个“多对一” RNN 网络，来执行基本的情绪分析，比如 “This is not happy” 属于负向情绪。

8.1.2 如何实现

让我们考虑“多对多”的 RNN 网络，它的输入为 \( x_0, x_1, \dots, x_{n-1}, x_n \) ，想要产生的输出为 \( y_0, y_1, \dots, y_{n-1}, y_n \) 。 \(x_i\) 和 \(y_i\) 都是向量，可以任意长度。

RNN 通过迭代中间隐藏状态 \(h\) 工作，\(h\) 是一个任意维度的向量。初始时，没有隐藏状态，\(h_0\) 使用随机值进行初始化，通过输入 \(x_0\) 和 \(h_0\) 计算输出 \(y_0\) 。在任意给定步骤 \(t\) ：

下一个隐藏状态 \(h_t\) 可以通过之前的隐藏状态 \(h_{t-1}\) 和下一个输入 \(x_t\) 计算出来。
下一个输出 \(y_t\) 可以使用 \(h_t\) 计算。

以上操作让 RNN 具有循环性：它在每个步骤中使用相同的权重。更具体地说，一个典型的基础循环神经网络仅使用 3 组权重来执行计算：

\(W_{xh}\) ，用于所有 \(x_t\) -> \(h_t\) 连接；
\(W_{hh}\) ，用于所有 \(h_{t-1}\) -> \(h_t\) 连接；
\(W_{hy}\) ，用于所有 \(h_t\) -> \(y_t\) 连接。

我们的 RNN 网络还有两个偏置：

\(b_h\) ，用于计算 \(h_t\) 的相加操作；
\(b_y\) ，用于计算 \(y_t\) 的相加操作。

使用矩阵表示权重，使用向量表示偏置，上面 3 组权重和 2 组偏置就能构成一个完整的 RNN 。下面公式将所有的参数放在一起：

\(h_t = tanh(W_{xh} \cdot x_t + W_{hh} \cdot h_{t-1} + b_h)\)

\(y_t = W_{hy} \cdot h_t + b_y\)

注：不要跳过这些等式，停下来思考一分钟，记住这些权重是矩阵，其它变量是向量。

所有权重都使用矩阵乘法计算，并将偏置添加到乘积结果中。使用 tanh 作为第一个激活函数（也可以使用其它激活函数，如 sigmoid 函数）。如果不知道什么是激活函数，第 4.2 节激活函数详细地介绍了它们。

8.1.3 问题

让我们开始动手吧！将从头开始实现一个 RNN 网络来执行简单的情感分析任务：确定给定的文本字符串的情绪是正向 (Positive) 的，还是负向 (Negative) 的。

文件 pos_peg.py 存放全部的样本数据，以 Python 字典的形式，包含训练集 train_data 和测试集 test_data ：

test_data = {
    'this is happy': True,
    'i am good': True,
    'this is not happy': False,
    'i am not good': False,
    'this is not bad': True,
    'i am not sad': True,
    'i am very good': True,
}

下表是一小部分样本数据：

Text	Positive?
I am good	✓
I am bad	❌
This is very good	✓
This is not bad	✓
I am bad not good	❌
I am not at all happy	❌
This was good earlier	✓
I am not at all bad or sad right now	✓

8.1.4 计划

由于这是一个分类问题，我们将使用“多对一”的 RNN 。这与我们之前讨论的“多对多”的 RNN 类似，但它仅使用最后的隐藏状态产生一个输出 \(y\) ：

每个 \(x_i\) 都是个向量，表示文本中的单词。输出 \(y\) 是一个包含两个数字的向量，一个代表正向情绪，另一个代表负向情绪。我们将应用 softmax 函数将这些值转换为概率，并最终在正向 / 负向之间做出判断。

让我们开始构建 RNN 模型！

8.1.5 预处理

之前提到的数据集包含两个 Python 字典结构：train_data 和 test_data 。我们需要对数据进行预处理，将它转换为可用的形式。对数据集里面存在的单词，构建一个单词表 vocab ，使用单词表中的下标表示单词。

# Create the vocabulary
vocab = list(set([w for text in pos_peg.train_data.keys() for w in text.split(' ')]))
vocab_size = len(vocab)
print('%d unique words found' % vocab_size)
print('Vocab:', vocab)

可以运行文件 1_5_pre_process.py 查看具体的情况，因为使用的 Python 语言 set 结构体，内部是无序的，所以每次程序执行，每个单词都能获取到不同的下标值：

18 unique words found
Vocab: ['now', 'and', 'or', 'good', 'not', 'sad', 'is', 'right', 'was', 'earlier',
    'at', 'very', 'am', 'i', 'bad', 'this', 'all', 'happy']

注：set 结构体会自动过滤到重复的单词。

vocab 包含训练集中至少出现一次的所有单词，现在可以使用对应的整数表示单词表中的单词，这是必要的，因为 RNN 不能理解文本，我们必须给它输入数字。

# Assign indices to each word.
word_to_idx = { w: i for i, w in enumerate(vocab) }
idx_to_word = { i: w for i, w in enumerate(vocab) }
print('Word of good index is', word_to_idx['good'])
print('First word is "' + idx_to_word[0] + '"')

上述代码生成了两个 dict 结构体，使用第一个结构体查看单词 good 的下标，使用第二个结构体查看下标 0 是哪个单词：

Word of good index is 3
First word is "now"

之前提到过每个输入 \(x_i\) 都是一个向量，这里我们使用独热 (One-Hot) 向量进行编码，用于将离散的单词数据编码成向量的形式。每个单词由一个独特的向量表示，其中只有一个位置为1，其他位置为0。

假设有三个类别：“Cat” ，“Dog” ，“Rabbit” ，对应的索引为 0，1，2 。那么 “Cat” 的 one-hot 向量为 [1, 0, 0] ，“Dog” 的 one-hot 向量为 [0, 1, 0] 。

因为在字典里有 18 个不同的单词，所以每个 \(x_i\) 的 one-hot 向量长度为 18 。使用 create_inputs 将文本数据转换为向量输入传递到神经网络中：

def create_inputs(text):
    '''
    Return an array of one-hot vectors representing the words
    in the input text string.
    - text is a string
    - each one-hot vector has shape (vocab_size, 1)
    '''
    inputs = []
    for w in text.split(' '):
        v = numpy.zeros((vocab_size, 1))
        v[word_to_idx[w]] = 1
            inputs.append(v)
    return inputs

比如将 “i am not at all good” 编码成为输入矩阵，得到的形状为 (6, 18, 1) 。

inputs = create_inputs('i am not at all good')
print('Input data shape', numpy.array(inputs).shape)

第一个维度大小表示句子中单词的个数，第二个维度表示词汇表中单词的个数，注意第三个维度的大小为 1 ，主要是便于后续计算。

8.1.6 前向传播

让我们开始实现 RNN 网络。使用标准正态分布，初始化 3 组权重值和 2 组偏置：

class RNN:
    # A vanilla recurrent neural network.
    def __init__(self, vocab_size, output_size, hidden_size=64):
        rng = numpy.random.default_rng(seed=0)
        self.Whh = rng.standard_normal((hidden_size, hidden_size)) / 1000
        self.Wxh = rng.standard_normal((hidden_size, vocab_size)) / 1000
        self.Why = rng.standard_normal((output_size, hidden_size)) / 1000
        self.bh = numpy.zeros((hidden_size, 1))
        self.by = numpy.zeros((output_size, 1))

注：我们将初始化的值除以 1000 ，这并不是一个最佳做法，但是它对于本模型非常简单且有效。

接下来实现 RNN 网络的前向传播，记住下面两个公式：

\(h_t = tanh(W_{xh} \cdot x_t + W_{hh} \cdot h_{t-1} + b_h)\)

\(y_t = W_{hy} \cdot h_t + b_y\)

文件 1_6_rnn_forward.py 将它们用代码实现：

def forward(self, inputs):
    '''
    Perform a forward pass of the RNN using the given inputs.
    Inputs is an array of one-hot vectors with shape (word_size, vocab_size, 1).
    Returns the final output and hidden state.
    '''
    h = numpy.zeros((self.Whh.shape[0], 1))
    # Perform each step of the RNN.
    for _, x in enumerate(inputs):
        h = numpy.tanh(self.Wxh @ x + self.Whh @ h + self.bh)
        # Compute the output.
        y = self.Why @ h + self.by
    return y, h

看上去非常简单？注意第一步我们将 \(h\) 初始化为零向量，因为在那之前没有隐藏状态。

当我们的第一个输入单词为 \(x \in \mathbb{R}^{18 \times 1}\) 时，下述公式可以看到网络的维度变化：

\(h \in \mathbb{R}^{64 \times 1} = tanh(W_{xh} \in \mathbb{R}^{64 \times 18} \cdot x \in \mathbb{R}^{18 \times 1} + W_{hh} \in \mathbb{R}^{64 \times 64} \cdot h \in \mathbb{R}^{64 \times 1} + b_h \in \mathbb{R}^{64 \times 1})\)

\(y \in \mathbb{R}^{2 \times 1} = W_{hy} \in \mathbb{R}^{2 \times 64} \cdot h \in \mathbb{R}^{64 \times 1} + b_y \in \mathbb{R}^{2 \times 1}\)

以此类推，直到最后一个单词，经过 softmax 函数转换为概率值，完成网络的前向传播过程：

rnn = RNN(vocab_size, 2)
inputs = create_inputs('i am very good')
out, h = rnn.forward(inputs)
porbs = softmax(out)
print(porbs)

传递 “i am very good” 看看网络的输出情况：

[[0.4999993]
 [0.5000007]]

此时网络起作用了，输出两个相近的概率值，但是并没有什么用，接下来使用反向传播进行训练！

8.1.7 反向传播

以下部分假设你具有微积分的基本知识，如果不想看，可以跳过它，但是我建议你不要跳过。如果你没有这部分背景，可以阅读第 4.1 节导数的内容。即使只是大概地浏览计算过程，对于理解循环神经网络也是有帮助的。

8.1.7.1 损失函数

为了训练我们的 RNN ，需要有损失函数，这里选择交叉熵损失函数，它经常和 softmax 函数一起使用，具体介绍查看第 4.3.3 小节交叉熵损失的内容，计算规则如下：

\(loss = - \sum_{i=1}^n y_i \ln(p_i)\)

\(n\) 表示类别数量；
\(y_i\) 是目标分布的真实标签，如果属于类别 \(i\) ，则 \(y_i = 1\) ，否则 \(y_i = 0\) ；
\(p_i\) 是模型预测属于类别 \(i\) 的概率（通过 softmax 得到的概率值）。

在本例中，目标分布有 [0, 1] 和 [1, 0] 两种情况，[0, 1] 表示目标为正向情绪的类别，[1, 0] 表示目标为负向情绪的类别。对于单个样本，如果真实类别为 \(c\) ，只有对应的 \(y_c = 1\) ，其它为 0。因此可以将上面公式进行简化：

\(l = - \ln(p_c)\)

其中 \(p_c\) 表示模型对正确类别（正向情绪或负向情绪）的预测概率。

比如文本预测出来的结果为 [0.1, 0.9] ，真实标签是正向的情绪，那么它的损失为：

\(l = -\ln(0.9) = 0.105\)

如果真实标签为负向情绪，那么它的损失为：

\(l = -\ln(0.1) = 2.302585\)

如果目标预测错误，那么它的损失较大。如果目标预测正确，那么它的损失接近于 0 。有了损失函数后，就可以用梯度下降最小化损失，这意味着需要对一些变量进行求导。

8.1.7.2 定义

对一些变量进行定义：

\(y\) 表示 RNN 神经网络的输出；
\(p\) 表示最后的概率：\(p = softmax(y)\) ；
\(c\) 表示文本的正确标签；
\(l\) 表示交叉熵损失：\(l = -\ln(p_c)\) ，\(p_c\) 是预测正确类别的概率；
\(W_{xh}\) ，\(W_{hh}\) 和 \(W_{hy}\) 表示 RNN 的 3 个权重矩阵；
\(b_h\) 和 \(b_y\) 表示 RNN 的 2 个偏置向量。

8.1.7.3 设置

另外我们需要在前向传播的过程中，存储一些数值，主要是每个单词的隐藏状态，用于反向传播的计算。构建反向传播的框架：

class RNN:
    def forward(self, inputs):
        h = numpy.zeros((self.Whh.shape[0], 1))
            
        self.last_inputs = inputs
        self.last_hs = { 0: h}
            
        # Perform each step of the RNN.
        for i, x in enumerate(inputs):
            h = numpy.tanh(self.Wxh @ x + self.Whh @ h + self.bh)
            self.last_hs[i + 1] = h
            # Compute the output.
            y = self.Why @ h + self.by
            return y, h

    def backprop(self, dy, learn_rate=2e-2):
        # dy (dl/dy) has shape (output_size, 1)
        pass

8.1.7.4 梯度

接下来是数学时间！梯度分为三个阶段进行计算：

第一个阶段计算损失 \(l\) 相对于输出 \(y\) 的梯度；
第二个阶段计算输出 \(y\) 相对于最后一个节点的隐藏状态 \(h_n\) 的梯度，同时更新参数 \(W_{hy}\) 和 \(b_y\) ；
第三个阶段是计算最后一个隐藏状态 \(h_n\) 相对于输入 \(x\) 的梯度，同时更新参数 \(W_{xh}\) 、\(W_{hh}\) 和 \(b_h\) 。

第一阶段计算 \(\frac{\partial l}{\partial y}\) ，根据公式：

\(l = -\ln(p_c) = -\ln(softmax(y_c))\)

\(l\) 关于 \(y_c\) 的偏导数，分两种情况讨论：当 \(i = c\) 和 \(i \ne c\) ：

1. 当 \(i = c\) （目标类别）

\(\frac{\partial l}{\partial y_c} = \frac{\partial (-ln(p_c))}{\partial y_c}\) ，利用链式法则：\(\frac{\partial l}{\partial y_c} = \frac{\partial l}{\partial p_c} \cdot \frac{\partial p_c}{\partial y_c}\)

交叉熵损失函数的导数公式为：\(\frac{\partial l}{\partial p_c} = - \frac{1}{p_c}\)

softmax 的导数公式为：\(\frac{\partial p_c}{\partial y_c} = p_c(1 - p_c)\)

代入得到 \(\frac{\partial l}{\partial y_c} = -\frac{1}{p_c} \cdot p_c \cdot (1 - p_c) = p_c - 1\)
2. 当 \(i \ne c\) （非目标类别）

\(\frac{\partial l}{\partial y_c} = \frac{\partial (-ln(p_c))}{\partial y_c}\) ，同样利用链式法则：\(\frac{\partial l}{\partial y_c} = \frac{\partial l}{\partial p_c} \cdot \frac{\partial p_c}{\partial y_c}\)

softmax 的导数公式为：\(\frac{\partial p_c}{\partial y_i} = -p_c \cdot p_i\)

代入得到 \(\frac{\partial l}{\partial y_i} = -\frac{1}{p_c} \cdot (-p_c \cdot p_i) = p_i\)

注：分类别讨论主要是 softmax 函数的导数引起的。

经过计算我们得到损失 \(l\) 相对于输出 \(y\) 的梯度：

\( \frac{\partial l}{\partial y_i} = \left\{ \begin{array}{ll} p_i - 1 & \text{if } i = j \\ p_i & \text{if } i \neq j \end{array} \right. \)

比如我们有一个概率 \(p = [0.2, 0.2, 0.6]\) ，正确得分类为 \(c = 0\) ，那么可以得到 \(\frac{\partial l}{\partial y} = [-0.8, 0.2, 0.6]\) 。这很容易转化为代码：

def process(data, backprop=True):
    items = list(data.items())
    random.shuffle(items)
        
    loss = 0
    num_correct = 0
        
    for x, y in items:
        inputs = create_inputs(x)
        target = int(y)
        
        # forward
        out, _ = rnn.forward(inputs)
        probs = softmax(out)
        
        # calculate loss / accuracy
        loss -= numpy.log(probs[target])
        num_correct += int(numpy.argmax(probs) == target)
        
        if backprop:
            # build dl/dy
            dl_dy = probs
            dl_dy[target] -= 1
        
            # backward
            rnn.backprop(dl_dy)

第二阶段需要计算 \(W_{hy}\) 和 \(b_y\) 的梯度，它们是唯一将隐藏状态转换为输出的节点：

\(\frac{\partial l}{\partial W_{hy}} = \frac{\partial l}{\partial y} \cdot \frac{\partial y}{\partial W_{hy}}\)

根据公式 \(y = W_{hy} \cdot h_n + b_y\)

\(\frac{\partial y}{\partial W_{hy}} = h_n\)，其中 \(h_n\) 是最后的隐藏状态，因此可以得到：

\(\frac{\partial l}{\partial W_{hy}} = \frac{\partial l}{\partial y} \cdot h_n\)

同样 \(\frac{\partial y}{\partial b_y} = 1\) ，得到：

\(\frac{\partial l}{\partial b_y} = \frac{\partial l}{\partial y}\)

如下使用代码表示：

def backprop(self, dy, learn_rate=2e-2):
    # dy (dl/dy) has shape (output_size, 1)
    n = len(self.last_inputs)
        
    # calculate dl/dwhy and dl/dby
    dwhy = dy @ self.last_hs[n].T
    dby = dy

第三阶段需要计算每一步的 \(W_{hh}\) ，\(W_{xh}\) 和 \(b_h\) 的梯度，我们有下面公式：

\(\frac{\partial l}{\partial W_{xh}} = \frac{\partial l}{\partial y} \sum_{t=0}^{n} (\frac{\partial y}{\partial h_t} \cdot \frac{\partial h_t}{\partial W_{xh}}) \)

因为改变 \(W_{xh}\) 会影响每个 \(h_t\) ，通过影响 \(y\) 值，最终影响损失 \(l\) 。为了计算 \(W_{xh}\) 的梯度，我们需要对所有的 \(t\) 进行反向传播，这就是著名的 时间上反向传播 (Backpropagation Through Time, BPTT) 。

上述公式需要分别计算 \(\frac{\partial y}{\partial h_t}\) 和 \(\frac{\partial h_t}{\partial W_{xh}}\) 的梯度。

\(W_{xh}\) 在所有的 \(x_t\) -> \(h_t\) 连接中都用到，所以要对所有的此类连接进行反向传播。对于给定步骤 \(t\) ，我们需要计算 \(\frac{\partial h_t}{\partial W_{xh}}\) ：

\(h_t = tanh(W_{xh} \cdot x_t + W_{hh} \cdot h_{t-1} + b_h)\)

其中，我们知道 \(\frac{d \tanh(x)}{dx} = 1 - \tanh^2(x)\) ，因此

\(\frac{\partial h_t}{\partial W_{xh}} = (1 - h_t^2)x_t\)

同样根据上述公式对其它两个参数进行求导得到：

\(\frac{\partial h_t}{\partial W_{hh}} = (1 - h_t^2)h_{t-1}\)

\(\frac{\partial h_t}{\partial b_h} = (1 - h_t^2)\)

最后需要 \(\frac{\partial y}{\partial h_t}\) ，我们可以使用循环计算：

\(\frac{\partial y}{\partial h_t} = \frac{\partial y}{\partial h_{t+1}} \cdot \frac{\partial h_{t+1}}{\partial h_t} = \frac{\partial y}{\partial h_{t+1}} \cdot (1 - h_t^2) \cdot W_{hh}\)

BPTT 的实现从最后一个隐藏状态开始，然后反向传递。因此当我们想要计算 \(\frac{\partial y}{\partial h_t}\) 时，已经计算出 \(\frac{\partial y}{\partial h_{t+1}}\) 的值，除了最后一个状态 \(h_n\) ：

\(\frac{\partial y}{\partial h_n} = W_{hy}\)

现在我们已经有了实施 BPTT 需要的一切参数，文件 1_7_rnn_backward.py 用代码实现 RNN 的反向传播：

class RNN:
    # ...
    def backprop(self, dy, learn_rate=2e-2):
        # dy (dl/dy) has shape (output_size, 1)
        n = len(self.last_inputs)
            
        # calculate dl/dwhy and dl/dby
        dwhy = dy @ self.last_hs[n].T
        dby = dy
                    
        # initialize dl/dwhh, dl/dwxh, and dl/dbh to zero
        dwhh = numpy.zeros(self.Whh.shape)
        dwxh = numpy.zeros(self.Wxh.shape)
        dbh = numpy.zeros(self.bh.shape)

        # calculate dl/dh for the last h
        # dl/dh = dl/dy * dy/dh
        dh = self.Why.T @ dy

        # backpropagation through time
        for t in reversed(range(n)):
            # an intermediate value: dl/dh * (1 - h^2)
            temp = ((1 - self.last_hs[t+1] ** 2) * dh)
            # dl/db = dl/dh * (1 - h^2)
            dbh += temp
            # dl/dwhh = dl/dh * (1 - h^2) * h_{t-1}
            dwhh += temp @ self.last_hs[t].T
            # dl/dwxh = dl/dh * (1 - h^2) * x
            dwxh += temp @ self.last_inputs[t].T
            # next dl/dh = dl/dh * (1 - h^2) * Whh
            dh = self.Whh.T @ temp
        
        # clip to prevent exploding gradients
        for d in [dwxh, dwhh, dwhy, dbh, dby]:
            numpy.clip(d, -1, 1, out=d)
    
        # update weights and biases using gradient descent
        self.Whh -= learn_rate * dwhh
        self.Wxh -= learn_rate * dwxh
        self.Why -= learn_rate * dwhy
        self.bh -= learn_rate * dbh
        self.by -= learn_rate * dby

有几点需要注意的是：

为了方便，使用 \(\frac{\partial l}{\partial h}\) 直接代替 \(\frac{\partial l}{\partial y} \cdot \frac{\partial y}{\partial h}\) 。
为了计算 \(\frac{\partial l}{\partial h_t}\) ，不停地更新 dh 的值，它存储最新计算出来的 \(\frac{\partial l}{\partial h_{t+1}}\) 的值。
结束 BPTT 后，使用 numpy.clip() 去掉梯度在 -1 以下，或者 +1 以上的值。这有助于缓解梯度爆炸问题，即由于存在大量乘项导致梯度变得非常大。梯度爆炸或消失对于普通 RNN 来说是个问题 - 更复杂的 RNN （如 LSTM）通常更有能力处理它们。
一旦计算出所有梯度，就使用梯度下降来更新权重和偏差。

我们已经成功完成 RNN 的反向传播！

8.1.8 测试

终于到了激动人心的时刻，接下来就需要对 RNN 网络进行测试，编写一个辅助函数：

def process(data, backprop=True):
    items = list(data.items())
    random.shuffle(items)

    loss = 0
    num_correct = 0

    for x, y in items:
        inputs = create_inputs(x)
        target = int(y)

        # forward
        out, _ = rnn.forward(inputs)
        probs = softmax(out)

        # calculate loss / accuracy
        loss -= numpy.log(probs[target])
        num_correct += int(numpy.argmax(probs) == target)

        if backprop:
            # build dl/dy
            dl_dy = probs
            dl_dy[target] -= 1

            # backward
            rnn.backprop(dl_dy)
    # Convert NumPy scalar to Python scalar.
    if isinstance(loss, numpy.ndarray):
        loss = loss.item()
    return loss / len(data), num_correct / len(data)

编写训练循环：

losses = []
accuracies = []
# training loop
for epoch in range(500):
    train_loss, train_acc = process(pos_peg.train_data)
    if (epoch + 1) % 50 == 0:
        losses.append(train_loss)
        accuracies.append(train_acc)
        print('Epoch %d' % (epoch + 1))
        print('Train: loss %.3f | accuracy: %.3f' % (train_loss, train_acc))

        test_loss, test_acc = process(pos_peg.test_data, backprop=False)
        print('Test: loss %.3f | accuracy: %.3f' % (test_loss, test_acc))

跑程序文件 1_7_rnn_backward.py 会得到一些输出，像下面这样：

Epoch 20
Train: loss 0.693 | accuracy: 0.552
Test: loss 0.698 | accuracy: 0.500
Epoch 40
Train: loss 0.692 | accuracy: 0.552
Test: loss 0.697 | accuracy: 0.500
Epoch 60
Train: loss 0.692 | accuracy: 0.552
Test: loss 0.696 | accuracy: 0.500
Epoch 80
Train: loss 0.692 | accuracy: 0.552
Test: loss 0.699 | accuracy: 0.500
Epoch 100
Train: loss 0.689 | accuracy: 0.534
Test: loss 0.697 | accuracy: 0.500

绘制训练过程的损失和精确度变化：

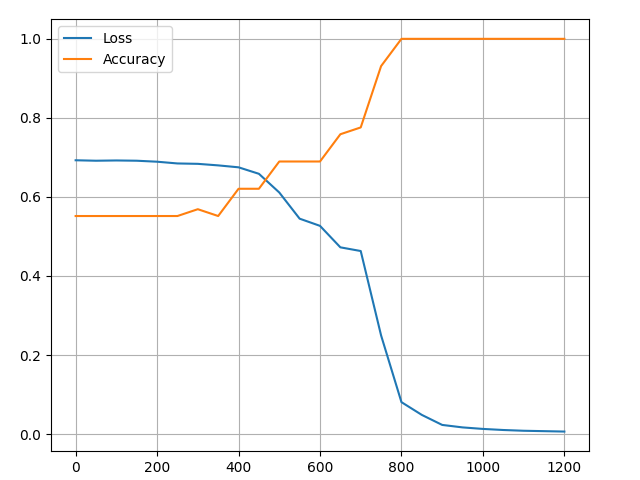
可以看到训练损失逐渐降低，训练精度逐渐提高，最终达到平衡，训练结束。

训练完成后，使用新的用例进行预测:

(predict, _) = rnn.forward(create_inputs('i am good'))
print('Predict text "i am good":', softmax(predict))

查看结果：

Predict text "i am good": [[0.01181507] [0.98818493]]

这就是全部！在这节中，我们经历了循环神经网络的整个过程，包括它们是什么、如何工作、它们为什么有用、如何训练它们以及如何实现。我们还可以做得更多：

了解长短期记忆网络（LSTM ，一种更强大、更流行的 RNN 架构）或门控循环单元（GRU，LSTM 的著名变体）。
使用机器学习库，（如 TensorFlow 、PyTorch 、JAX ）实验更大/更好的数据。
阅读有关双向 RNNs 的信息，它可以处理正向的和反向序列，以便为输出层提供更多的信息。
尝试使用词嵌入 (Word Embedding) ，比如 GloVe 或 Word2Vec ，它可以将语句转换为更有用的向量表示。

8.1.9 PyTorch 实现

文件 1_9_rnn_torch.py 使用 PyTorch 实现 RNN 架构，对文本进行正向和负向分类的完整示例，其中核心代码为：

# 定义模型
class RNNClassifier(torch.nn.Module):
    def __init__(self, vocab_size, embedding_dim, hidden_dim, output_dim):
        super(RNNClassifier, self).__init__()
        self.embedding = torch.nn.Embedding(vocab_size, embedding_dim)
        self.rnn = torch.nn.RNN(embedding_dim, hidden_dim, batch_first=True)
        self.dense = torch.nn.Linear(hidden_dim, output_dim)
    
    def forward(self, x):
        embedded = self.embedding(x)
        _, hidden = self.rnn(embedded)
        # 取最后一个隐藏状态
        hidden = hidden[-1]
        out = self.dense(hidden)
        return out

代码说明：

数据预处理：文本被编码为词索引，并填充到固定长度 (max_len) 。
RNN 模型使用嵌入层 (nn.Embedding) 将词索引映射为向量，使用 (nn.RNN) 构建循环神经网络。用全连接层 (nn.Linear) 将隐藏状态映射为分类结果。
训练与测试：通过 DataLoader 迭代数据，使用交叉熵损失函数优化模型。

和手写 RNN 的逻辑基本一致。

运行代码：

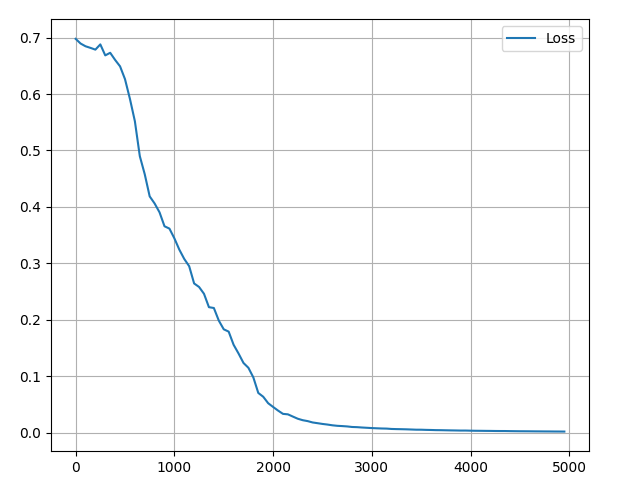
Epoch 1/100, loss: 0.6992
Epoch 11/100, loss: 0.6679
Epoch 21/100, loss: 0.4506
Epoch 31/100, loss: 0.2457
Epoch 41/100, loss: 0.0999
Epoch 51/100, loss: 0.0307
Epoch 61/100, loss: 0.0142
Epoch 71/100, loss: 0.0086
Epoch 81/100, loss: 0.0059
Epoch 91/100, loss: 0.0041

损失逐渐降低，最终接近 0 ，非常好的结果。下图是绘制的损失变化图像：