8.2 RNN 详解

从头构建 RNN 语言生成模型，理解时间反向传播 (BPTT) ，实现 GRU/LSTM 网络！

创建日期: 2025-01-20

循环神经网络（RNN）是一种流行的模型，在许多 NLP 任务中都表现出了巨大的潜力。尽管它们最近很受欢迎，但我只找到了有限数量的资源来彻底解释 RNN 的工作原理以及如何实现它们。这就是本教程的内容，它由多个部分组成的系列，我计划在其中介绍以下内容：

• 1. RNN 介绍；

• 2. 使用 NumPy 实现 RNN；

• 3. 理解时间反向传播 (BPTT) 算法和梯度消失问题；

• 4. 实现 GRU/LSTM RNN 网络。

作为本教程的一部分，我们将实现一个基于循环神经网络的语言模型。语言模型的应用有两个方面：首先，它允许我们根据句子在现实世界中出现的可能性对任意句子进行评分。这为我们提供了语法和语义正确性的衡量标准，此类模型通常用作机器翻译系统的一部分。其次，语言模型允许我们生成新文本（我认为这是更酷的应用）。在莎士比亚数据集上训练的语言模型使我们能够生成类似莎士比亚的文本。

我假设你对基础神经网络有所了解。如果不熟悉，可以去阅读 第 02 章 深度学习原理 的内容，它将指导我们了解非循环网络背后的思想和实现。

8.2.1 RNN 介绍

本小节简单地介绍 RNN 是什么，常见的 RNN 结构，以及有哪些用途。

8.2.1.1 什么是 RNN

RNN 背后的想法是利用顺序信息，在传统的神经网络中，我们假设所有的输入（和输出）都是相互独立的。但对于许多任务来说，这是一个坏主意，如果你想预测句子中的下一个单词，你最好知道它之前有哪些单词。

RNN 之所以被称为“循环”，是因为它们对序列的每个元素执行相同的任务，而输出取决于之前的计算。另一种思考 RNN 的方式是，它们有一个“记忆”，可以捕获已经被计算的信息。理论上，RNN 可以利用任意长度序列中的信息，但实际上它们仅限于回顾固定的数量（稍后会详细解释）。典型的 RNN 如下所示：

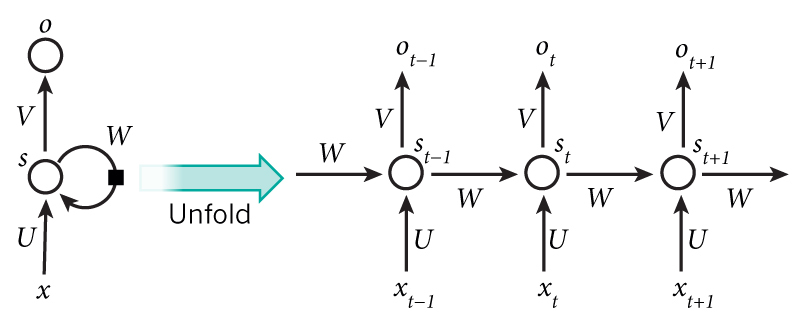
上图显示了一个正在被展开的 RNN 网络。展开的意思是我们将整个网络的序列写出来。假设我们关心的序列是一个包含 5 个单词的句子，则网络将展开为 5 层，每个单词一层。控制 RNN 中发生计算的公式如下：

• \(x_t\) 是在步骤 \(t\) 时刻的输入。比如，\(x_1\) 是句子中第二个单词的独热向量。

• \(s_t\) 是在步骤 \(t\) 时刻的隐藏状态，相当于网络的记忆。\(s_t\) 的计算基于之前的隐藏状态和当前步骤的输入：\(s_t = f(U \cdot x_t + W \cdot s_{t-1})\) 。函数 \(f\) 通常是非线性的 tanh 或者 ReLU 激活函数。\(s_{-1}\) 用于计算第一个隐藏状态，所有数值初始化为零。

• \(o_t\) 对应步骤 \(t\) 时刻的输出，比如我们想要预测句子中的下一个单词，它将是我们词汇表中的概率向量，\(o_t = softmax(V \cdot s_t)\) 。

有几点需要注意的是：

• 我们可以认为隐藏状态 \(s_t\) 是网络的记忆，\(s_t\) 捕获有关之前所有时间步骤中发生的信息。输出 \(o_t\) 仅根据当时的记忆 \(s_t\) 来计算。正如前面说到的，现实情况会更复杂些，因为 \(s_t\) 不能获取太久之前步骤的信息。

• 与在每一层使用不同的参数的传统深度神经网络不同，在所有步骤中，RNN 共享相同的参数 \((U, V, W)\) 。这反映了我们在每个步骤中执行的相同的任务，只是输入不同。这大大减少我们需要学习的参数总量。

• 上图在每个时间步骤都有输出，但根据任务的不同，这可能不是必需的。例如在预测句子的情绪时，只关心最终输出，而不是每个单词后的情绪。同样，我们可能不需要每个时间步骤的输入。RNN 的主要特征是其隐藏状态，它捕获序列的一些信息。

8.2.1.2 能做什么

RNN 在许多 NLP 任务中都取得了巨大成功，现在我应该提到，最常用的 RNN 类型是 LSTM ，它在捕获长期依赖性方面比普通 RNN 好得多。但别担心，LSTM 本质上与我们将在本教程中开发的 RNN 相同，只是它们计算隐藏状态的方式不同。我们将在后面的小节中更详细地介绍 LSTM。以下是 RNN 在 NLP 领域的一些示例应用，这绝不是一份详尽的清单。

语言建模和生成文本

给定一个单词序列，我们想要根据之前已经给定的单词预测每个单词的概率。语言模型使我们能够衡量句子的相似度，这是机器翻译的重要输入（高相似度的句子通常是正确的）。能够预测下一个单词的副作用是我们得到了一个生成模型，它使我们能够通过从输出概率中采样，来生成新文本。并且根据我们的训练数据，可以生成各种各样的东西。在语言建模中，我们的输入通常是单词序列（例如编码为独热向量），我们的输出是预测单词的序列。在训练网络时，设置 \(o_t = x_{t+1}\) ，因为我们想 \(t\) 时刻的输出将是下个单词。

机器翻译

机器翻译与语言建模类似，因为我们的输入是源语言（例如德语）中的单词序列。我们希望输出是目标语言（例如英语）中的单词序列。一个关键的区别是，我们的输出只有在我们看到完整的输入后才开始，因为我们翻译的句子的第一个单词可能需要从完整的输入序列中捕获信息。

以下是关于机器翻译的研究论文：

• Sequence to Sequence Learning with Neural Networks

• Neural Machine Translation by Jointly Learning to Align and Translate

语音识别

给定来自声波信号作为输入序列，我们可以预测一系列语音片段及其概率。

生成图像描述

RNN 与卷积神经网络一起被用作模型的一部分，用于生成未标记图像的描述。这种方法的效果非常惊人。组合模型甚至将生成的单词与图像中的特征进行对齐。

8.2.1.3 训练 RNN

训练 RNN 与训练传统神经网络类似。我们也使用反向传播算法，但略有不同。由于网络中的所有时间步骤共享参数，因此每个输出处的梯度不仅取决于当前时间步骤的计算，还取决于先前的时间步骤。例如想要计算时刻 \(t = 4\) 的梯度，我们需要反向传播 3 个时刻，并将这些梯度加起来。这叫做 时间反向传播 (BPTT) 。如果这还不太清楚，别担心，我们后续会介绍细节。现在，只需注意这样一个事实：使用 BPTT 训练的普通 RNN 难以学习长期依赖关系（例如相距很远的步骤之间的依赖关系），这是由于所谓的梯度消失或爆炸引起的。存在一些机制来处理这些问题，某些类型的 RNN（如 LSTM）是专门为解决该问题而设计的。

8.2.1.4 RNN 拓展

多年来，研究人员开发了更复杂的 RNN 类型来处理普通 RNN 模型的一些缺点。我们将在后续文章中更详细地介绍它们，但我希望本节作为简要概述，以便您熟悉模型的分类。

双向 RNN

基于以下的思想：时刻 \(t\) 的输出可能不仅取决于序列中的前一个元素，还取决于未来的元素。例如，要预测序列中缺失的单词，您需要同时查看左侧和右侧上下文。双向 RNN 非常简单。它们只是两个堆叠在一起的 RNN。然后根据两个 RNN 的隐藏状态计算输出。

LSTM 网络

如今非常流行，我们在上面简要介绍了它们。LSTM 的架构与 RNN 并无根本区别，但它们使用不同的函数来计算隐藏状态。LSTM 中的记忆称为单元，我们可以将它想象成为一个黑盒子，将之前的状态 \(h_{t-1}\) 和当前的输入 \(x_t\) 作为输入。单元内部决定哪些记忆被保留，哪些被擦除。然后结合之前的状态、当前的记忆和输入产生输出。这些单元在在捕获长期依赖关系方面非常有效。

8.2.2 实现 RNN

这个小节我们将使用 Python 从头开始实现一个完整的循环神经网络。会跳过一些对于理解循环神经网络来说并非必不可少的样板代码，但所有的代码都在 Github 仓库 上。

8.2.2.1 语言建模

我们的目标是使用循环神经网络构建语言模型，这意味着如果我们有 m 个单词的句子，语言模型使我们能够预测观察句子（在给定数据集中）的概率，如下所示：

\(P(w_1, ... , w_m) = \prod_{i=1}^mP(w_i|w_1, ..., w_{i-1})\)

用文字来说，一个句子的概率是每个单词在给定前面的单词情况下的概率的乘积。因此，句子“He went to buy some chocolate” 中 “chocolate” 的概率由 “He went to buy some” 中 “some” 乘以 “He went to buy” 的概率得到，以此类推。

这有什么用呢？为什么我们要为观察一个句子分配的概率呢？

首先，这种模型可以用作评分机制。例如，机器翻译系统通常会为输入的句子生成多个候选句子。你可以使用语言模型来挑选最可能的句子。直观地看，最可能的句子很可能是语法正确的。语音识别系统也会发生类似的评分。

但解决语言建模还有一个很酷的副作用。因为我们可以根据前面的单词预测单词的概率，所以我们能够生成新的文本，这是一个生成模型。给定一个现有的单词序列，我们从预测的概率中抽取下一个单词，并重复该过程，直到我们得到一个完整的句子。

请注意，在上面的等式中，每个单词的概率取决于所有先前的单词。实际上，由于计算或内存限制，许多模型很难表示这种长期依赖关系。他们通过常仅限于查看前面几个单词。RNN 理论上可以捕捉这种长依赖关系，但实际上它有点复杂，我们将在后续探讨这一点。

8.2.2.2 数据与预处理

为了训练我们的语言模型，需要文本来学习。幸运的是，我们不需要任何标签来训练语言模型，只需要原始文本。数据集 REDDIT 收集了 15000 条较长的 reddit 评论，我们的模型生成的文本看起来像 reddit 评论者（希望如此）。与大多数机器学习项目一样， 首先需要进行一些预处理，以使我们的数据变成正确的格式。

1. 1. 标记文本

我们有原始文本，但我们希望基于每个单词的预测，这意味着我们必须将评论转变为句子，句子转变为单词。可以用空格分割每个评论，但这样无法正确处理标点符号。句子 “He left!” 应该有 3 个标记：“He”，“left”，“!” 。使用 NLTK 库的 sent_tokenize 和 word_tokenize 方法，它会为我们做很多工作。

1. 2. 删除低频单词

我们文本中的大多数单词只会出现一两次。删除这些不常见的单词是个好主意。词汇量过大会使我们的模型训练速度变慢（稍后会讨论为什么会这样），而且由于我们没有很多此类单词的上下文示例，无论如何都无法学习如何正确使用它们。这与人类的学习方式非常相似。要真正理解如何恰当地使用一个单词，你需要在不同的上下文中看到它。

在代码中，我们会通过 vocabulary_size 限制单词表的词汇量（这里设置为 8000，可以任意地修改它）。没有包含在词汇表中的单词使用 UNKNOWN_TOKEN 表示。比如单词 “nonlinearities” 不在我们的词汇表中，那么句子 “nonlineraties are important in neural networks” 就会变成 “UNKNOWN_TOKEN are important in Neural Networks” 。单词 UNKNOWN_TOKEN 会进入词汇表，就像我们预测其它单词一样。当我们生成新文本时，可以将 UNKNOWN_TOKEN 替换掉，比如随机选取一个不在单词表里的单词，或者我们生成的句子到出现 UNKNOWN_TOKEN 为止。

1. 3. 开始和结束标记

我们还想了解哪些单词往往是句子的开头和结尾。为此在前面添加一个特殊的 SENTENCE_START 标记，在句子的末尾添加一个 SENTENCE_END 标记。这使我们能够提出以下问题：假设第一个标记是 SENTENCE_START ，那么下一个可能的单词是什么，即句子实际的第一个单词。

1. 4. 构建数据矩阵

循环神经网络的输入是向量，而不是字符串。因此我们在单词和索引之间创建映射，定义 index_to_word 和 word_to_index 变量。比如单词 “friendly” 的索引可能为 2001 。一个训练样本 \(x\) 可能像 [0, 179, 341, 416] 这样，其中 0 对应的是 SENTENCE_START 。对应的标签 \(y\) 为 [179, 341, 416, 1] 。请记住，我们的目标是预测下一个单词，因此 \(y\) 只是 \(x\) 向量向前移动一个为止，最后一个元素是标记 SENTENCE_END 。换句话说，对于单词 179 正确的预测是 341 ，表示下一个单词。

vocabulary_size = 8000
unknown_token = 'UNKNOWN_TOKEN'
sentence_start_token = 'SENTENCE_START'
sentence_end_token = 'SENTENCE_END'
nltk.download('punkt_tab')
# Read the data and append SENTENCE_START and SENTENCE_END tokens.
print('Reading CSV files...')
with open('temp/reddit-comments-2015-08.csv', 'r', encoding='utf-8') as f:
    reader = csv.reader(f, skipinitialspace=True)
    # Split full comments into sentences.
    sentences = itertools.chain(*[nltk.sent_tokenize(x[0].lower()) for x in reader])
    # Append SENTENCE_START and SENTENCE_END.
    sentences = ['%s %s %s' % (sentence_start_token, x, sentence_end_token) for x in sentences]
print('Parsed', len(sentences), 'sentences')

# Tokenize the sentences into words.
tokenized_sentences = [nltk.word_tokenize(sent) for sent in sentences]
# Count the word frequencies.
word_freq = nltk.FreqDist(itertools.chain(*tokenized_sentences))
print('Found', len(word_freq.items()), 'unique words tokens')

# Get the most common words and build index_to_word and word_to_index vectors.
vocab = word_freq.most_common(vocabulary_size - 1)
index_to_word = [x[0] for x in vocab]
index_to_word.append(unknown_token)
word_to_index = dict([(w, i) for i, w in enumerate(index_to_word)])
print('Using vocabulary size', vocabulary_size)
print('The least frequent word in our vocabulary is', vocab[-1][0], 'and appeared', vocab[-1][1], 'times')

# Replace all words in our vocabulary with the unkown token.
for i, sent in enumerate(tokenized_sentences):
    tokenized_sentences[i] = [w if w in word_to_index else unknown_token for w in sent]

print('Example sentence 10:', sentences[10])
print('Example sentence 10 after pre-processing:', tokenized_sentences[10])

# Create the training data.
x_train = numpy.asarray([[word_to_index[w] for w in sent[:-1]] for sent in tokenized_sentences], dtype=object)
y_train = numpy.asarray([[word_to_index[w] for w in sent[1:]] for sent in tokenized_sentences], dtype=object)
print('Sentence 10 source:', x_train[10])
print('Sentence 10 target:', y_train[10])

上述代码主要是实现上面 4 个步骤，可以执行文件 2_2_text_preprocess.py 查看输出结果：

Parsed 79185 sentences
Found 63011 unique words tokens
Using vocabulary size 8000
The least frequent word in our vocabulary is whitebeard and appeared 10 times
Example sentence 10: SENTENCE_START a dishonest seller isn't going to run the check in the first place. SENTENCE_END
Example sentence 10 after pre-processing: ['SENTENCE_START', 'a', 'dishonest', 'seller', 'is', "n't", 'going', 'to', 'run', 'the', 'check', 'in', 'the', 'first', 'place', '.', 'SENTENCE_END']
Sentence 10 source: [0, 7, 7510, 3415, 13, 17, 126, 5, 327, 3, 329, 14, 3, 132, 269, 2]
Sentence 10 target: [7, 7510, 3415, 13, 17, 126, 5, 327, 3, 329, 14, 3, 132, 269, 2, 1]

8.2.2.3 理解公式

上一个小节中描述了 RNN 网络的总体架构。接下来具体一点，看看我们的语言模型是什么样子的。输入 \(x\) 是一系列的单词（像之前打印的示例那样），每个 \(x_t\) 是一个单词。但注意有一点：由于矩阵乘法的工作原理，我们不能简单地使用单词索引（如 36）作为输入。相反将每个单词表示大小为 vocabulary_size 的独热向量。我们在神经网络代码中执行此转换，而不是预处理中。网络输出 \(o\) 有类似的格式，每个 \(o_t\) 是一个 vocabulary_size 大小的向量，每个元素表示该词成为句子中下一个词的概率。

让我么回顾一下上一个小节 RNN 的方程：

\(s_t = tanh(U \cdot x_t + W \cdot s_{t-1})\)

\(o_t = softmax(V \cdot s_t)\)

我发现记录矩阵和向量的维度很有用，假设我们选择的词汇量大小 \(C = 8000\) ，隐藏层的大小 \(H = 100\) ，可以将隐藏层看作是网络的记忆。让隐藏层更大可以学习到更复杂的模式，但是也增加了额外的计算。那么有下面的记号：

\(x_t \in \mathbb{R}^{8000}\)

\(o_t \in \mathbb{R}^{8000}\)

\(s_t \in \mathbb{R}^{100}\)

\(U \in \mathbb{R}^{100 \times 8000}\)

\(V \in \mathbb{R}^{8000 \times 100}\)

\(W \in \mathbb{R}^{100 \times 100}\)

它们是很重要的信息，记住 \(U\) 、\(V\) 和 \(W\) 是我们网络想要从数据中进行学习的参数。因为我们总共需要学习 \(2HC+H2\) 个参数，在 \(C = 8000\) 和 \(H = 100\) 时那就是 1610000 个。维度也告诉我们模型的瓶颈。注意因为 \(x_t\) 是独热向量，和 \(U\) 进行相乘，需要 \(U\) 的列数和它是相同的。网络中最大的矩阵是 \(V \cdot s_t\) ，这就是我们为什么将词汇量设置得比较小的原因。

有了这些，我们就可以开始代码实现！

8.2.2.4 初始化

首先声明一个 RNN 类并初始化我们的参数。参数 U、V 和 W 的初始化有点儿棘手。我们不能直接将它们初始化为 0，因为这会导致我们所有层的结果都是零。必须随机初始化它们，由于适当的初始化似乎对训练结果有影响，因此在这方面已经有很多研究。事实证明，最佳初始化取决于激活函数（我们的例子使用 tanh 函数），将初始值设置在如下区间：

\([-\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}}]\)

其中 \(n\) 是前一层的连接数量，这听起来有点麻烦。但别担心，初始化一个随机很小的值也是可以的。

class RNNNumpy:
    def __init__(self, word_dim, hidden_dim=100, bptt_truncate=4):
        # Assign instance variables.
        self.word_dim = word_dim
        self.hidden_dim = hidden_dim
        self.bptt_truncate = bptt_truncate
        # Randomly initialize the network parameters.
        rng = numpy.random.default_rng(0)
        self.U = rng.uniform(-numpy.sqrt(1./word_dim), numpy.sqrt(1./word_dim),
                                (hidden_dim, word_dim))
        self.V = rng.uniform(-numpy.sqrt(1./hidden_dim), numpy.sqrt(1./hidden_dim),
                                (word_dim, hidden_dim))
        self.W = rng.uniform(-numpy.sqrt(1./hidden_dim), numpy.sqrt(1./hidden_dim),
                                (hidden_dim, hidden_dim))

上面 word_dim 是我们词汇表的大小，hidden_dim 是隐藏层的数量。现在不用担心 bptt_truncate 参数，稍后会详细解释它。

8.2.2.5 前向传播

接下来是前向传播，通过上面定义的公式，预测单词的概率：

def forward_propagation(self, x):
    # The total number of time steps.
    T = len(x)
    # During forward propagation we save all hidden states in s because need them later.
    # We add one additional element for the initial hidden, which we set to 0.
    s = numpy.zeros((T + 1, self.hidden_dim))
    # The outputs at each time step. Again, we save them for later.
    o = numpy.zeros((T, self.word_dim))

    # For each time step...
    for t in numpy.arange(T):
        # Note that we are indexing U by x[t].
        # This is the same as multiplying U with a one-hot vector.
        s[t] = numpy.tanh(self.U[:, x[t]] + self.W.dot(s[t-1]))
        o[t] = softmax(self.V.dot(s[t]))
    return (o, s)

不仅返回计算的输出，还返回隐藏状态。我们稍后会使用它们来计算梯度，通过在这里返回，我们可以避免重复计算。每个 \(o_t\) 是一个表示词汇表中单词的概率向量，但有时，例如在评估模型时，我们想要的只是下一个概率最高的单词，称此为 predict 函数：

def predict(self, x):
    # Perform forward propagation and return index of the highest score.
    o, s = self.forward_propagation(x)
    return numpy.argmax(o, axis=1)

让我们尝试一下新实现的方法，运行 2_2_rnn_forward.py 文件：

model = RNNNumpy(vocabulary_size)
(o, s) = model.forward_propagation(x_train[10])
print('Output shape:', o.shape)

predictions = model.predict(x_train[10])
print('Prediction shape:', predictions.shape)
print('Prediction', predictions)

查看示例输出：

Output shape: (16, 8000)
Prediction shape: (16,)
Prediction [6703 1153 4245  857 3803 1813 6387 2065 7020 4074  140  877 4765 1913
    1111  557]

对于句子中的每个单词（上面的 16 个），我们的模型做出了 8000 个预测，代表下一个单词的概率。请注意，因为我们初始化了 \(W\), \(U\) 和 \(V\) 随机值，这些预测现在完全是随机的， numpy.argmax 函数给出每个单词最高概率预测的索引。

8.2.2.6 计算损失

为了训练我们的网络，我们需要一种方法来衡量它所犯的错误，称之为损失函数。我们的目标是从训练数据中找到参数 \(U\) 、\(V\) 和 \(W\) 使得损失函数最小。损失函数一个常用的选择是交叉熵损失。如果我们有 \(N\) 个训练样本（句子数量）和 \(C\) 个分类（词汇表的大小），那么我们的预测的输出 \(o\) 和真实标签 \(y\) 的损失，通过下面公式计算：

\(l(y, o) = - \frac{1}{n} \sum_{i=1}^n y_i \log(o_i)\)

这个公式看起来有点复杂，但它实际上做的就是对我们的训练样本求和，并根据我们的预测的偏差程度增加损失。真实标签 \(y\) 和 预测 \(o\) 离得越远，那么损失就越大，下面实现 calculate_loss 函数：

# 同时传递多个句子
    def calculate_total_loss(self, x, y):
        loss = 0
        # For each sentence...
        for i in numpy.arange(len(y)):
            (o, s) = self.forward_propagation(x[i])
            # We only care about our prediction of the 'correct' words.
            correct_word_predictions = o[numpy.arange(len(y[i])), y[i]]
            # Add to the loss based on how off we are.
            loss += -1 * numpy.sum(numpy.log(correct_word_predictions))
        return loss
    
    def calculate_loss(self, x, y):
        # Divide the total loss by the number of training examples.
        N = 0
        for y_i in y:
            N += len(y_i)
        return self.calculate_total_loss(x, y) / N

让我们退一步思考一下随机预测的损失应该是多少。这将为我们提供一个基准，并确保我们的实现是正确的。我们的词汇表中有 、\(C = 8000\) 个单词，那么平均每个单词的预测概率为 1/8000 ，那么它将会产生损失 \(l = -\frac{1}{N}Nlog(\frac{1}{c}) = log(c)\) 。

print('Expect loss:', numpy.log(vocabulary_size))
loss = model.calculate_loss(x_train[:1000], y_train[:1000])
print('Actual loss:', loss)

执行上面你的语句：

Expect loss: 8.987196820661973
Actual loss: 8.9871760879241

非常接近！请记住，评估整个数据集的损失是一项昂贵的操作，如果您有大量数据，则可能需要几个小时！

8.2.2.7 BPTT 梯度

记住我们要在训练集上找到参数 \(U\) 、\(V\) 和 \(W\) 使损失值最小，最常见的方法是随机梯度下降法 (SGD) 。SGD 背后的想法非常简单，我们迭代所有训练示例，在每次迭代中，将参数推向减少误差的方向。这些方向由损失的梯度给出：

\(\frac{\partial l}{\partial U} , \frac{\partial l}{\partial V} , \frac{\partial l}{\partial W}\)

SGD 还需要一个学习率，它定义了我们在每个迭代步骤中想要迈出多大的步长。SGD 是不仅适用于神经网络，也适用于许多其他机器学习算法。因此，已经有很多关于如何使用批处理、并行和自适应学习率来优化 SGD 的研究。尽管基本思想很简单，但以真正有效的方式实现 SGD 可能会变得非常复杂。我将实现一个简单版本的 SGD，即使没有优化背景也应该可以理解。

但是我们如何计算上面提到的梯度呢？在传统的神经网络中，我们通过反向传播算法来实现这一点。在 RNN 中，我们使用这个算法的一个稍微修改过的版本，称为时间反向传播 (BPTT)。因为参数由网络中的所有时间步骤共享，所以每个输出的梯度不仅取决于当前时间步骤的计算，还取决于之前的时间步骤。如果你懂微积分，那其实就是应用链式法则。本教程的下一部分将全部关于 BPTT，所以我就不在这里详细推导了。上一个小节已经推导过，过程基本一致。

现在你可以把 BPTT 当作一个黑匣子。它将训练示例 \((x, y)\) 作为输入 , 并返回梯度 \(\frac{\partial l}{\partial U}\) ，\(\frac{\partial l}{\partial V}\) ，\(\frac{\partial l}{\partial W}\) 。

def bptt(self, x, y):
    T = len(y)
    # Perform forward propagation.
    (o, s) = self.forward_propagation(x)
    # We accumulate the gradients in these variables.
    dldU = numpy.zeros(self.U.shape)
    dldV = numpy.zeros(self.V.shape)
    dldW = numpy.zeros(self.W.shape)
    delta_o = o
    delta_o[numpy.arange(len(y)), y] -= 1.0
    # For each output backwards.
    for t in numpy.arange(T)[::-1]:
        dldV += numpy.outer(delta_o[t], s[t].T)
        # Initial delta calculation.
        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t]**2))
        # Backpropagation through time (for at most self.bptt_trancate steps)
        for bptt_step in numpy.arange(max(0, t - self.bptt_truncate), t+1)[::-1]:
            dldW += numpy.outer(delta_t, s[bptt_step-1])
            dldU[:, x[bptt_step]] += delta_t
            # Update delta for next step.
            delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
    return (dldU, dldV, dldW)

注：和上一个小节中 backprop 函数非常相似，只不过这个会有多个输出。

每当你实现反向传播时，最好也实现梯度检查，这是一种验证你的实现是否正确的方法。梯度检查背后的想法是：参数的导数等于该点的斜率，我们可以通过稍微改变参数然后除以变化来近似：

\(\frac{\partial l}{\partial θ} \approx \lim_{h \to 0}\frac{J(θ + h - J(θ - h))}{2h}\)

然后，我们将使用反向传播计算出的梯度与使用上述方法估计出的梯度进行比较。如果没有太大差异，那就没问题了。近似需要计算每个参数的总损失，因此梯度检查非常昂贵（请记住，在上面的例子中我们有超过一百万个参数）。因此，最好在词汇量较小的模型上执行它。

def gradient_check(self, x, y, h=0.001, error_threshold=0.01):
    # Calculate the gradients using backpropagation. We want to checker if these are correct.
    bptt_gradients = self.bptt(x, y)
    # List of all parameters we want to check.
    model_parameters = ['U', 'V', 'W']
    # Gradient check for each parameter
    for pidx, pname in enumerate(model_parameters):
        # Get the actual parameter value from the mode, e.g. model.W
        parameter = operator.attrgetter(pname)(self)
        # Iterate over each element of the parameter matrix, e.g. (0,0), (0,1), ...
        it = numpy.nditer(parameter, flags=['multi_index'])
        while not it.finished:
            ix = it.multi_index
            # Save the original value so we can reset it later
            original_value = parameter[ix]
            # Estimate the gradient using (f(x+h) - f(x-h))/(2*h)
            parameter[ix] = original_value + h
            gradplus = self.calculate_total_loss([x],[y])
            parameter[ix] = original_value - h
            gradminus = self.calculate_total_loss([x],[y])
            estimated_gradient = (gradplus - gradminus)/(2*h)
            # Reset parameter to original value
            parameter[ix] = original_value
                # The gradient for this parameter calculated using backpropagation
            backprop_gradient = bptt_gradients[pidx][ix]
            # calculate The relative error: (|x - y|/(|x| + |y|))
            relative_error = numpy.abs(backprop_gradient - estimated_gradient) 
            # If the error is to large fail the gradient check.
            if relative_error > error_threshold * (numpy.abs(backprop_gradient) + numpy.abs(estimated_gradient)):
                print('Gradient check error: parameter = ' + pname + ', ix = ' + str(ix))
                print('+h loss:', gradplus)
                print('-h loss:', gradplus)
                print('Estimated_gradient:', estimated_gradient)
                print('Backpropagation gradient:', backprop_gradient)
                print('Relative error:', relative_error)
                return
            it.iternext()
        print('Gradient check for parameter ' + pname + ' passed')

将词汇量设置为 100 ，检查梯度计算是否正确：

grad_check_vocab_size = 100
model = RNNNumpy(grad_check_vocab_size, 10, bptt_truncate=1000)
model.gradient_check([1, 2, 3, 5], [2, 3, 4, 5])

三个参数全部通过：

Gradient check for parameter U passed
Gradient check for parameter V passed
Gradient check for parameter W passed

现在我们能够计算参数的梯度，可以实现 SGD 了。分两步来做：1. 一个函数 sgd_step，计算梯度并执行一批更新。2. 一个外循环，迭代训练集并调整学习率。

def sgd_step(self, x, y, learning_rate):
    # Calculate the gradients
    dldU, dldV, dldW = self.bptt(x, y)
        # Change parameters according to gradients and learning rate
    self.U -= learning_rate * dldU
    self.V -= learning_rate * dldV
    self.W -= learning_rate * dldW

def train_with_sgd(model, x_train, y_train, learning_rate=0.005, epochs=100, evaluate_loss_after=5):
    losses = []
    num_examples_seen = 0
    for epoch in range(epochs):
        # Optionally evaluate the loss
        if epoch % evaluate_loss_after == 0:
            loss = model.calculate_loss(x_train, y_train)
            losses.append((num_examples_seen, loss))
            print('Loss after num_example_seen=' + str(num_examples_seen) + ' epoch=' + str(epoch) + ' - ' + str(loss))
            # Adjust the learning rate if loss increases.
            if len(losses) > 1 and losses[-1][1] > losses[-2][1]:
                learning_rate = learning_rate * 0.5
        # For each training example...
        for i in range(len(y_train)):
            model.sgd_step(x_train[i], y_train[i], learning_rate)
            num_examples_seen += 1

完成了！让我们试着了解一下训练网络需要多长时间：

model = RNNNumpy(vocabulary_size)
start = time.time()
model.sgd_step(x_train[10], y_train[10], 0.005)
duration = time.time() - start
print('Train 10 samples duration:', duration)

哦，坏消息。在我的笔记本电脑上，SGD 的一步大约需要 0.1165556 毫秒。我们的训练数据中有大约 80,000 个示例，因此一个 epoch（对整个数据集的迭代）需要几个小时。多个 epoch 需要几天甚至几周的时间！而且，与许多公司和研究人员使用的数据集相比，我们仍在使用一个小数据集。现在怎么办？

Train sample 10 duration: 0.077613592

幸运的是，有很多方法可以加快我们的代码。我们可以坚持使用相同的模型并让我们的代码运行得更快，或者我们可以修改我们的模型以降低计算成本，或者两者兼而有之。研究人员已经发现了许多降低模型计算成本的方法，例如使用分层 softmax 或添加投影层以避免大型矩阵乘法。

查看下模型在小型数据集上的运行过程，这里只选取 100 个样本：

# Train on a small subset of the data to see what happen
model = RNNNumpy(vocabulary_size)
losses = train_with_sgd(model, x_train[:100], y_train[:100], epochs=10, evaluate_loss_after=1)

下面的训练结果可以看到损失在逐步降低：

Loss after num_example_seen=0 epoch=0 - 8.98699959020797
Loss after num_example_seen=100 epoch=1 - 8.97546552759948
Loss after num_example_seen=200 epoch=2 - 8.95878875276646
Loss after num_example_seen=300 epoch=3 - 8.927849164429205
Loss after num_example_seen=400 epoch=4 - 8.854070798624434
Loss after num_example_seen=500 epoch=5 - 6.851557379210689
Loss after num_example_seen=600 epoch=6 - 6.259403789928947
Loss after num_example_seen=700 epoch=7 - 5.974928366514176
Loss after num_example_seen=800 epoch=8 - 5.7997245132120785
Loss after num_example_seen=900 epoch=9 - 5.680167565188178

8.2.2.8 文本生成

现在我们有了模型，我们可以让它为我们生成新文本！让我们实现一个辅助函数来生成新句子：

def generate_sentence(model):
    # We start the sentence with the start token.
    new_sentence = [int(word_to_index[sentence_start_token])]
    # Repeat until we get an end token.
    while not new_sentence[-1] == word_to_index[sentence_end_token]:
        (next_word_probs, _) = model.forward_propagation(new_sentence)
        sampled_word = word_to_index[unknown_token]
        # We don't want to sample unknown words.
        while sampled_word == word_to_index[unknown_token]:
            samples = numpy.random.multinomial(1, next_word_probs[-1])
            sampled_word = int(numpy.argmax(samples))
        new_sentence.append(sampled_word)
    sentence_str = [index_to_word[x] for x in new_sentence[1:-1]]
    return sentence_str

# predict words
num_sentences = 10
sentence_min_length = 7
for i in range(num_sentences):
    sent = []
    while len(sent) < sentence_min_length:
        sent = generate_sentence(model)
    print(' '.join(sent))

看看生成的句子，有几件有趣的事情值得注意。该模型成功地学习了语法。它正确地放置了逗号并用标点符号结束句子。有时它会模仿互联网语音，例如多个感叹号或笑脸。

Anyway, to the city scene you’re an idiot teenager.
What ? ! ! ! ! ignore!
Screw fitness, you’re saying: https
Thanks for the advice to keep my thoughts around girls.
Yep, please disappear with the terrible generation.

然而，生成的句子中绝大多数都没有意义或有语法错误（我确实在上面挑选了最好的句子）。一个原因可能是我们没有训练网络足够长的时间或没有使用足够的训练数据。这可能是真的，但很可能不是主要原因。我们的原始 RNN 无法生成有意义的文本，因为它无法学习相隔几步的单词之间的依赖关系。这也是为什么 RNN 在刚发明时未能流行的原因。它们在理论上很漂亮，但在实践中效果不佳。

幸运的是，现在人们对训练 RNN 的困难有了更好的了解。在下一部分中，我们将更详细地探讨时间反向传播 (BPTT) 算法，并演示所谓的梯度消失问题。这将促使我们转向更复杂的 RNN 模型，例如 LSTM，它是 NLP 中许多任务的最新技术（并且可以生成更好的 reddit 评论！）。您在本教程中学到的所有内容也适用于 LSTM 和其它 RNN 模型，因此如果原始 RNN 的结果比您预期的更差，请不要灰心。

8.2.3 理解 BPTT 算法

在上一个小节中，我们从头开始实现了 RNN，但没有详细介绍时间反向传播 (BPTT) 算法如何计算梯度。在本部分中，我们将简要概述 BPTT，并解释它与传统反向传播的不同之处。然后，我们将尝试理解消失梯度问题，该问题导致了 LSTM 和 GRU 的发展，这两个模型是目前在 NLP（和其他领域）中使用的最流行和最强大的模型。

为了充分理解本教程的这一部分，我建议熟悉偏微分和基本反向传播的工作原理。

8.2.3.1 BPTT 算法

让我们快速回顾一下 RNN 的基本方程。请注意有个小改变就是将 \(o\) 换成 \(\hat{y}\)，和一些常见的文献保持一致：

\(s_t = tanh(U \cdot x_t + W \cdot s_{t-1})\)

\(\hat{y_t} = softmax(V \cdot s_t)\)

我们还将损失（或误差）定义为交叉熵损失，其公式如下：

\(E_t(y_t, \hat{y_t}) = -y_tlog\hat{y_t}\)

\(E(y, \hat{y}) = \sum_{t=1}^nE_t(y_t, \hat{y_t}) = -\sum_{t=1}^ny_tlog\hat{y_t}\)

这里，\(y_t\) 是时间步骤 \(t\) 时刻正确的单词，\(\hat{y_t}\) 是我么你的预测。通常将整个序列（句子）当作一个训练样本，因此总的错误是每一个时间步骤（单词）的错误相加得到的。

请记住，我们的目标是计算误差相对于参数 \(U\) 、\(V\) 和 \(W\) 的梯度，使用SGD 进行学习。就像我们在每个时间步骤将错误相加一样，在每个训练样本上，我们也将梯度相加：\(\frac{\partial E}{\partial W} = \sum_{t=1}^n\frac{\partial E_t}{\partial W}\) 。

为了计算这些梯度，我们使用链式微分法则。这是从误差开始向前传播。接下来使用 \(E_3\) 作为示例，这样有具体的数字可以参考：

\(\frac{\partial E_3}{\partial V} = \frac{\partial E_3}{\partial \hat{y_3}} \cdot \frac{\partial \hat{y_3}}{\partial V}\)

\(= \frac{\partial E_3}{\partial ŷ} \cdot \frac{\partial ŷ_3}{\partial z_3} \cdot \frac{\partial z_3}{\partial V} = (ŷ_3 - y_3) ⊗ s_3\)

上面 \(z_3 = V \cdot s_3\) ，⊗ 表示两个向量的外积。如果你不动上面的也不要担心，我跳过了几个步骤，你可以似乎用微分计算它们（非常好的练习）。这里我想表达的是 \(\frac{\partial E_3}{\partial V}\) 只和当前时间步骤的 \(ŷ_3)，\(y_3\) 和 \(s_3\) 相关。如果你有这些值，俺么计算相对于 \(V\) 的梯度就是一个简单的矩阵。

求解对 \(W\) 和 \(U\) 的梯度有些不同，我们可以像上面一下写下链式规则：

\(\frac{\partial E_3}{\partial W} = \frac{\partial E_3}{\partial ŷ_3} \cdot \frac{\partial ŷ_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial W}\)

从公式 \(s_3 = tanh(U \cdot x_t + W \cdot s_2)\) 可以看到上述梯度计算还取决于 \(s_2\) ，\(s_2\) 又取决于 \(W\) 和 \(s_1\) ，以此类推。如果我们考虑 \(W\) 的梯度就不能将 \(s_2\) 看作是一个常量。我们需要继续使用链式法则，看它到底发生了什么：

\(\frac{\partial E_3}{\partial W} = \sum_{k=0}^3\frac{\partial E_3}{\partial ŷ_3} \cdot \frac{\partial ŷ_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial s_k} \cdot \frac{\partial s_k}{\partial W}\)

我们将每个时刻对梯度的贡献加起来，换句话说，因为 \(W\) 在我们计算每一步输出前都会用到，我们需要计算从 \(t = 3\) 的梯度到 \(t = 0\) 的反向梯度。

请注意，这与我们在深度前馈神经网络中使用的标准反向传播算法完全相同。关键区别在于，我们将相对于 \(W\) 的梯度在每个时间步骤相加。在传统的 NN 中，我们不跨层共享参数，因此我们不需要求和。但这也意味着 BPTT 只是展开的 RNN 上的标准反向传播的花哨名称。就像反向传播一样，你可以定义反向的增量，比如：\(δ_2^3 = \frac{\partial E_3}{\partial z_2} = \frac{\partial E_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial s_2} \cdot \frac{\partial s_2}{\partial z_2}\) ，其中 \(z_2 = U \cdot x_2 + W \cdot s_1\) ，然后应用相同的等式。

一个 BPTT 的简单实现会像下面这个样子：

def bptt(self, x, y):
    T = len(y)
    # Perform forward propagation.
    (o, s) = self.forward_propagation(x)
    # We accumulate the gradients in these variables.
    dldU = numpy.zeros(self.U.shape)
    dldV = numpy.zeros(self.V.shape)
    dldW = numpy.zeros(self.W.shape)
    delta_o = o
    delta_o[numpy.arange(len(y)), y] -= 1.0
    # For each output backwards.
    for t in numpy.arange(T)[::-1]:
        dldV += numpy.outer(delta_o[t], s[t].T)
        # Initial delta calculation.
        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t]**2))
        # Backpropagation through time (for at most self.bptt_trancate steps)
        for bptt_step in numpy.arange(max(0, t - self.bptt_truncate), t+1)[::-1]:
            dldW += numpy.outer(delta_t, s[bptt_step-1])
            dldU[:, x[bptt_step]] += delta_t
            # Update delta for next step.
            delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
    return (dldU, dldV, dldW)

这应该也能让你明白为什么标准 RNN 很难训练：序列（句子）可能很长，可能有 20 个单词或更多，因此你需要通过多层进行反向传播。实际上，许多人将反向传播截断为几个步骤。

8.2.3.2 梯度消失问题

之前提到 RNN 很难学习长距离依赖关系——相隔几步的单词之间的交互。这是有问题的，因为一个英文句子的含义通常由不太接近的单词决定：“The man who wore a wig on his head went inside”。这句话实际上是关于一个男人走进屋子，而不是关于假发。但普通的 RNN 不太可能捕捉到这样的信息。为了理解原因，让我们仔细看看上面计算的梯度：

\(\frac{\partial E_3}{\partial W} = \sum_{k=0}^3\frac{\partial E_3}{\partial ŷ_3} \cdot \frac{\partial ŷ_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial s_k} \cdot \frac{\partial s_k}{\partial W}\)

记住\(\frac{\partial s_3}{\partial s_k}\) 本身就需要链式法则计算！比如 \(\frac{\partial s_3}{\partial s_1} = \frac{\partial s_3}{\partial s_2} \cdot \frac{\partial s_2}{\partial s_1}\) 。还要注意，因为我们对向量函数求导，所以结果是一个矩阵（称为雅可比矩阵），其元素都是逐点导数。我们可以重写 \(\frac{\partial s_3}{\partial s_k}\) ：

\((\prod_{j=k+1}^3\frac{\partial s_j}{\partial s_{j-1}})\frac{\partial s_k}{\partial W}\)

我们的激活函数将所有的值都映射 [-1, 1] 的范围，并且导数的最大值是 1 （sigmoid 激活函数是 1/4 ）。

tanh 和 sigmoid 函数在两端的导数都是 0 ，它们接近一条水平线。当这发生时，我们说相应的神经元已经饱和。它们具有零梯度，并将前几层中的其它梯度推向 0 。在矩阵乘法中如果值较小，那么梯度值就会快速表小，最终在几个步骤中消失，然后那些状态就不再对学习起作用：结果就是无法学习长依赖。梯度消失并不是 RNN 独有的，它也发生在其它前馈网络中。只是 RNN 往往非常深（在我们的例子中，深度与句子长度相当），这使得这个问题很常见。

很容易想象，如果雅可比矩阵的值很大，那么根据我们的激活函数和网络参数，我们可能会得到梯度爆炸而不是梯度消失。事实上，这就是所谓的梯度爆炸问题。梯度消失比梯度爆炸更受关注的原因有两个。首先，梯度爆炸是显而易见的。你的梯度将变成 NaN （不是数字），你的程序会崩溃。其次，在预定义的阈值处剪切梯度是解决梯度爆炸的一个简单有效的做法。梯度消失更成问题，因为他们何时发生或如何处理并不明显。

幸运的是，有几种方法可以解决梯度消失问题。正确初始化 \(W\) 矩阵可以减少梯度消失。正则化也可以。一种更好的方法是使用 ReLU 而不是 tanh 和 sigmoid 激活函数。ReLU 激活函数的梯度是 0 或者是 1 ，因此它不容易有梯度消失问题。

一种更常用的做法是使用 LSTM 或者 GRU 架构。LSTM 在 1997 年就发表了，它可能是今天（2015年） NLP 领域用得最多的。GRU 发表于 2014 年，是 LSTM 的简化版。这两种 RNN 架构都是专门为处理梯度消失和有效学习长程依赖关系而设计的，将在本教程的下一部分中介绍它们。

8.2.4 实现 GRU/LSTM

本小节我们会学习 LSTM 和 GRU 网络，LSTM 发表于 1997 年，是当今 NLP 深度学习中最广泛使用的模型之一。GRU 于 2014年首次使用，是 LSTM 的更简单版本，具有很多相同的属性。让我们先了解一下 LSTM，再了解 GRU 的不同之处。

8.2.4.1 LSTM 网络

上个小节中，我们研究了梯度消失问题如何阻止基础的 RNN 学习长期依赖关系。LSTM 旨在通过门控机制对抗梯度消失。为了理解这意味着什么。让我们看看 LSTM 如何计算隐藏状态 \(s_t\) （使用空心圆 ∘ 表示逐元素乘法）：

\(i = σ(x_t \cdot U^i + s_{t-1} \cdot W^i)\)

\(f = σ(x_t \cdot U^f + s_{t-1} \cdot W^f)\)

\(o = σ(x_t \cdot U^o + s_{t-1} \cdot W^o)\)

\(g = tanh(x_t \cdot U^g + s_{t-1} \cdot W^g)\)

\(c_t = c_{t-1} ∘ f + g ∘ i\)

\(s_t = tanh(c_t) ∘ o\)

这些等式看起来复杂，但是如果花几分钟观察它们就不难理解。第一，LSTM 层只是另一种计算隐藏状态的方式，之前我们是通过 \(s_t = tanh(U \cdot x_t + W \cdot s_{t-1}\) 计算隐藏状态的。

对于这个单元来说输入是 t 时刻的输入 \(x_t\) 和之前的隐藏状态 \(s_{t-1}\) ，输出是新的隐藏状态 \(s_t\) 。LSTM 只是用不同的方式做相同的事情，这是理解模型的关键。

你可以将 LSTM 和 GRU 当作一个黑盒单元，给定当前的输入和之前的隐藏状态，它们以某种方式计算新的隐藏状态。

有了上面的直观的信息后，看看 LSTM 单元具体是怎么计算隐藏状态的。我这里只给出简单的解释，你可以阅读 这篇文章 获取更深的视角。总结如下：

• i , f , o 分别叫做输入、遗忘和输出门。注意它们有完全相同的等式，只是不同的参数矩阵。它们被称为门是因为 sigmoid 函数将向量值映射到 [0, 1] 的区间，通过和其它向量逐元素相乘，你可以定义其它向量通过多少比例。

  输入门定义要让多少当前的新计算通过，遗忘门定义让多少之前的状态通过，输出们定义要暴露多少内部状态给下一步。这些门有相同的维度 \(d_s\) ，隐藏状态的大小。

• g 是基于当前输入和前一个隐藏状态计算的“候选”隐藏状态，它与我们之前在普通 RNN 计算的方程完全相同，只是将参数 U 和 W 重新命名为 \(U^g\) 和 \(W^g\) 。然而并不是将 g 像之前一样作为新的隐藏状态，而是使用输入门来挑选一些。

• \(c_t\) 是单元的内部记忆，它是之前的记忆 \(c_{t-1}\) 和遗忘门进行相乘，然后再和计算出来的 g 相乘的结果。因此，直观地说，它是我们想要如何结合先前的记忆和新的输入的组合。我们可以完全忽略旧记忆（遗忘门全为 0) 或完全忽略新计算的状态 （输入门全为 0 ），但最有可能的是，我们希望在这两个极端之间找到某种东西。

• 对于记忆 \(c_t\) ，通过将记忆和输出门进行相乘，我们计算最终的隐藏状态 \(s_t\) 。并不是所有的内部记忆都会被网络中下一个隐藏状态使用。

直观地看，普通 RNN 可以被视为 LSTM 的一个特例。如果你将输入门固定为全 1，将遗忘门固定为全 0（你总是忘记之前的记忆），将输出门固定为全 1（你暴露整个记忆），你几乎就得到了标准的 RNN。只是多了一点 tanh 这会压缩输出。门控机制允许 LSTM 明确地模拟长期依赖关系。通过学习门控的参数，网络可以了解其内存应如何运行。

值得注意的是，基本 LSTM 架构存在几种变体。一种常见的变体是创建窥孔连接，使门不仅依赖于先前的隐藏状态 \(s_{t-1}\) ，而且还取决于先前的内部状态 \(c_{t-1}\) ，在门方程中添加一个附加项。

8.2.4.2 GRU 网络

GRU 层背后的思想与 LSTM 层非常相似，方程式也是如此：

\(z = σ(x_t \cdot U^z + s_{t-1} \cdot W^z)\)

\(r = σ(x_t \cdot U^r + s_{t-1} \cdot W^r)\)

\(h = tanh(x_t \cdot U^h + (s_{t-1} ∘ r) \cdot W^h)\)

\(s_t = (1 - z) ∘ h + z ∘ s_{t-1}\)

GRU 网络有两个门，一个重置门 r ，一个更新门 z 。重置门决定如何将新输入与先前的记忆相结合，而更新门则定义要保留多少先前的记忆。如果我们将重置设置为全 1，将更新门设置为全 0，我们就会再次得到普通的 RNN 模型。使用门控机制来学习长期依赖关系的基本思想与 LSTM 相同，但有几个关键区别：

• GRU 有两个门，LSTM 有 3 个门。

• GRU 不具备内部存储器 \(c_t\) ，它们没有 LSTM 中存在的输出门。

• 通过更新门 z 将输入门和遗忘门结合在一起，重置门直接应用之前的隐藏状态。

• 在计算输出时，没有应用第二个非线性函数。

8.2.4.3 实现

现在我们已经了解了两种解决梯度消失问题的模型，你可能会想：该使用哪一种？GRU 是相当新的（2014年），它们的权衡尚未得到充分探索。在许多任务中，这两种架构都产生了相当的性能，调整层大小等超参数可能比选择理想的架构更重要。GUR 的参数较少，因此可能训练得更快一些或需要更少得数据来概括。另一方面，如果你有足够得数据，LSTM 更强大得表达能力可能会带来更好得结果。

使用 PyTorch 实现，未完待续！