Transformer 论文

9.4 Transformer 论文

注意力 (Attention) ，你只需要它！

创建日期: 2025-01-23

论文作者：Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, Illia Polosukhin

主要的 序列转导模型 (Sequence Transduction Model) 基于复杂的循环或者卷积神经网络，它们包含一个 编码器 (Encoder) 和一个 解码器 (Decoder)。性能最佳的模型还通过 注意力机制 (Attention Mechanism) 连接编码器和解码器。我们提出一种新的简单的网络架构 Transformer ，它只基于注意力机制，完全省去了循环和卷积操作。

在两个 机器翻译 (Machine Translation) 任务上的实验表明，模型质量优越，并行性更高，并且训练时间明显减少。在 WMT 2014 英语翻译成德语的任务中，我们的模型获得 28.4 BLEU 分数，比现有最佳结果，包括 集成 (Ensemble) 模型，至少提高 2 BLEU 分数。在 WMT 2014 英语翻译成法语的任务中，我们的模型在 8 块 GPU 上训练了 3.5 天，达到了 41.8 BLEU 分数，创新了单模型最好成绩，其训练成本仅为其它最佳模型的一小部分。

WMT 是 Workshop on Machine Translation 的缩写，WMT 14 指的是 2014 年的机器翻译研讨会，它提供了 英-法 和 英-德 语言数据集。

BLEU 是一个自动评价机器翻译的方法，来自论文 BLEU: a Method for Automatic Evaluation of Machine Translation ，它通过比较机器翻译结果与人类参考翻译的 N-gram 重叠度来衡量翻译质量，分数越高表示翻译质量越好。

我们通过将 Transformer 成功应用于英语翻译（无论是大量还是有限训练数据的情况下），证明了 Transformer 能很好地泛化到其它任务。

8 位作者对论文有同等贡献，名字顺序是随机的，他们每个人所作的工作如下：

Jakob 建议用自注意力取代 RNN，并开始努力评估这一想法。
Ashish 和 Illia 设计并实现了第一个 Transformer 模型，并在该工作的方方面面都发挥了至关重要的作用。
Noam 提出了缩放点积注意力机制、多头注意力机制和无参位置表示，也参与了许多细节工作。
Niki 在我们的代码仓和 tensor2tensor （tensor2tensor 已经使用 trax 代替）中设计、实现、调整和评估了无数的模型变体。
Llion 也尝试了模型变体，负责最初的代码库设计以及高效的推理和可视化。
Lukasz 和 Aidan 花了无数个漫长的日子设计并实现了 tensor2tensor 的各个部分，替换了我们之前的代码库，大大改善了结果，并加快了研究。

9.4.1 介绍

循环神经网络，特别是长短期记忆 (LSTM) 和门控循环 (GRU) 神经网络，已经被认为是解决 序列建模 (Sequence Modeling)和转导问题（比如语言建模和机器翻译）的最先进方法。许多研究工作在持续推动循环语言模型和 编码器-解码器 (Encoder-Decoder) 架构的边界。

LSTM 来自于论文 Long Short-Term Memory ，GRU 来自于论文 Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling 。

语言建模、机器翻译和编码器-解码器相关研究论文：

循环模型通常根据输入和输出序列的符号位置进行计算。通过位置与计算时间步骤对齐，它们会生成一系列的隐状态 \(h_t\) ，它是之前隐状态 \(h_{t-1}\) 和位置 \(t\) 输入的函数。这种固有的顺序性阻碍了训练样本的并行化，这在较长的序列中尤其重要，因为内存限制了样本之间的批处理。

最近的研究通过 分解技巧 (Factoization Trick) 和 条件计算 (Conditional Computation) ，显著提高了计算效率，同时后者也能提高模型性能。然而，顺序计算的基本约束仍然存在。

分解技巧来自于论文 Factorization tricks for LSTM networks ，条件计算来自于论文 Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer 。

注意力机制已经称为序列建模和转导模型不可或缺的一部分，它允许对依赖关系进行建模，而无需考虑它们在输入或输出序列中的距离。然而，除了少数情况外，这种注意力机制都是与循环网络结合使用的。

论文 Neural Machine Translation by Jointly Learning to Align and Translate 和 Structured Attention Networks 使用注意力机制，论文 A Decomposable Attention Model for Natural Language Inference 使用注意力将问题分解成可以解决的子问题，实现并行化。

在这项工作中，我们提出了 Transformer ，这是一种避免循环、完全依靠注意力机制来绘制输入和输出之间的全局依赖关系的架构。Transformer 显著提高了并行化水平，在 8 个 P100 GPU 上训练 12 小时后，就可以达到最新的翻译质量水平。

9.4.2 背景

减少序列计算的目标也是 Extended Neural GPU 、ByteNet 和 ConvS2S 的基础，它们都使用卷积神经网络作为基本构建块，并行计算所有输入和输出位置的 隐藏表示 (Hidden Representation) 。在这些模型中，关联两个任意输入或输出位置的信号所需的操作数随着位置之间的距离而增加，对于 ConvS2s 呈线性增长，对于 ByteNet 呈对数增长。这使得学习远距离位置之间的依赖关系变得更加困难。

在 Transformer 中，这被减少到一个恒定数量的操作，尽管由于平均注意力加权位置而降低了有效分辨率，但我们使用第 9.4.3.2 小节注意力中描述的多头注意力来抵消这种影响。

自注意力 (Self-attention) 有时也称为内部注意力，是一种将单个序列的不同位置关联起来以计算该序列的表示的注意力机制。自注意力已成功用于各种任务，包括阅读裂解、抽象总结、语言推理和句子表示。

基于循环注意力机制，而非序列对齐循环的端到端记忆网络，已在简单语言问答和语言建模任务上取得良好表现。

然后，据我们所知，Transformer 是第一个完全依赖自注意力来计算其输入和输出表示的传导模型，而无需使用序列对齐的 RNN 或者 CNN 。在以下部分中，我们将描述 Transformer ，为什么使用自注意力，讨论相对于其它模型的优点。

9.4.3 模型架构

大多数具有竞争力的神经序列转导模型都具有编码器-解码器结构。这里，编码器将符号表示的输入序列 \((x_1, ... , x_n)\) 映射成连续表示的序列 \(z = (z_1, ... , z_n)\) 。给定 \(z\) ，解码器生成一个输出符号序列 \((y_1, ... , y_m)\) ，每次生成一个元素。在每个步骤中，模型都是自回归的，在生成下一个符号时将先前生成的符号作为附加输入。

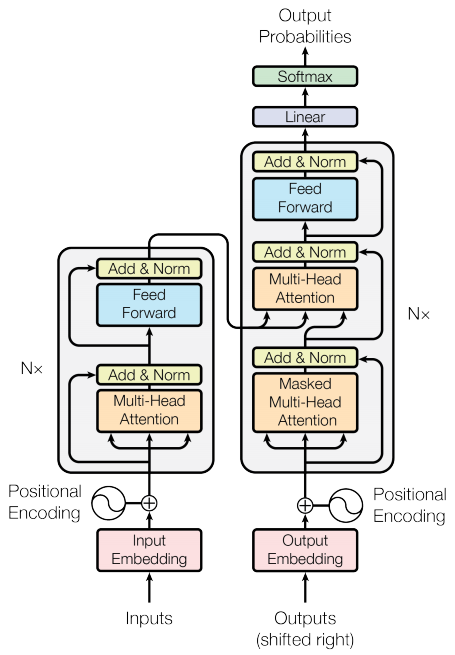
Transformer 整体架构如上图所示，编码器（左边）和解码器（右边）都使用多头自注意力和全连接层。

9.4.3.1 编码器和解码器栈

编码器 (Encoder) ：编码器由 \(N = 6\) 个相同层堆叠而成。每个层有两个子层，第一个子层是多头自注意力机制，第二个是简单的全连接前馈网络。两个子层都分别采用了残差连接，然后进行了层归一化。

也就是说，每个子层的输出为 LayerNorm(x + Sublayer(x)) ，其中 Sublayer(x) 是子层本身实现的函数。为了促进这些残差连接，模型中的所有子层，包括嵌入层，产生的输出维度都是 \(d_{model} = 512\) 。

解码器 (Decoder) ：解码器也由 \(N = 6\) 个相同的层堆叠而成，除了编码器的两个子层外，解码器还插入第三个子层，该子层对编码器的输出执行多头注意力。与编码器类似，我们在每个子层中采用残差连接，然后进行层归一化。

我们还修改了解码器堆栈中的自注意力子层，以防止在当前位置时关注后续位置。这种掩盖，加上输出偏移一个位置的事实，确保位置 \(i\) 的预测智能依赖于小于 \(i\) 的位置的已知输出。

9.4.3.2 注意力

一个注意力函数可以描述为将 查询 (Query) 和一组 键-值 (Key-Value) 对映射到输出，其中查询、键、值和输出都是向量。输出被计算成为值得加权和，其中分配给每个值得权重由查询与相应键得兼容性函数计算得出。

缩放点积注意力

我们称此论文的注意力为 缩放点积注意力 (Scale Dot-Product Attention) 。查询和键的维度是 \(d_k\) ，值的维度是 \(d_v\) ，它们组成输入。我们计算查询和所有键的点积，除以 \(\sqrt{d_k}\) ，使用 softmax 函数获取在值上的权重。

在实践中，我们同时在一系列的查询中计算注意力函数，将它合并成矩阵 \(Q\) ，键和值也分别合并成矩阵 \(K\) 和 \(V\) 。使用如下公式计算输出矩阵：

\(Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\)

最常用的两个注意力函数是加性注意力和点积注意力，点积注意力和我们的算法相似，除了缩放因子 \(\frac{1}{\sqrt{d_k}}\) 。加性注意力使用具有单个隐藏层的前馈网络来进行兼容性计算。虽然两者在理论上复杂度相似，但点积注意力在实践中更快、更节省空间，因为它可以使用高度优化的矩阵乘法来实现。

虽然对于较小的 \(d_k\) 值，两种机制得表现相似。但对于较大的 \(d_k\) 值，加法注意力优于点积注意力（没有除以 \(\sqrt{d_k}\)）。我们怀疑，对于较大的 \(d_k\) 值，点积的值会变大，从而将 softmax 推入具有极小梯度的区域。为了抵消这种影响，我们将点积乘以 \(\frac{1}{\sqrt{d_k}}\) 。

为了说明点积为何变大，假设 \(q\) 和 \(k\) 是独立的随机变量，它们的均值为 0 ，方差为 1 ，那么它们的点积 \(q \cdot k = \sum_{i=1}^{d_k}q_{i}k_i\) ，它的均值为 0 ，方差为 \(d_k\) 。

多头注意力

与其在维度为 \(d_{model}\) 的键、值和查询中执行单个注意力函数，我们发现将查询、键和值使用可学习参数将它们线性投影到 \(d_k\) 、\(d_k\) 和 \(k_v\) 维，重复上述操作 \(h\) 次，这样效果更好。然后在每个投影的查询、键和值上，并行执行注意力函数，得到 \(d_v\) 维度的输出值。这些值连接起来，再次投影，得到最终值。

多头注意力机制允许模型联合起来关注不同位置的不同表示子空间的信息。使用单个注意力头时，平均化会抑制这一点。

                \(MultiHead(Q, K, V) = Concat(head_1, ... , head_h)W^O\) 
 \(head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)\) 
            

其中投影是参数矩阵 \(W_i^Q \in R^{d_{model} \times d_k}\) ， \(W_i^K \in R^{d_{model} \times d_k}\) ， \(W_i^V \in R^{d_{model} \times d_v}\) 和 \(W^O \in R^{hd_v} \times d_{model}\) 。

在本工作中，我们采用了 \(h = 8\) 个并行注意力层，对于每个层，我们使用 \(d_k = d_v = d_{model} / h = 64\) ，由于每层的维度减小，总计算成本与具有全维度的单头注意力相似。

注意力在模型的应用

Transformer 通过三种不同的方式使用多头注意力机制：

在编码器-解码器注意力层，查询来自解码器，键和值来自编码器的输出。这允许解码器中的每个位置关注输入序列中的所有位置。模仿了序列到序列模型中的典型编码器-解码器注意机制。
编码器包含自注意力层，在自注意力层中，所有的键、值和查询都来自相同的地方，也就是说，编码器中的前一层输出。编码器中的每个位置都可以关注前一层的所有位置。
类似地，解码器中的自注意力层允许解码器中的每个位置关注当前位置之前的所有位置。我们需要防止解码器看到当前位置之后的位置，以保留自回归属性。我们在缩放点积注意力中实现了这一点，方式是将 softmax 中的非法输入设置为 \(-\infty\) 。

9.4.3.3 位置前馈网络

除了注意力子层之外，我们的编码器和解码器中的每一层都包含一个完全连接的前馈网络，该网络分别且相同地应用于每个位置。它由两个线性变换和其间的 ReLU 激活组成。

\(FFN(x) = max(0, xW_1 + b_1)W_2 + b_2\)

虽然线性变换在不同位置上是相同的，但它们在层与层之间使用不同的参数。另一种描述方式是将其作为两个卷积，内核大小为 1 。输入和输出的维度 \(d_{model} = 512\) ，内部隐藏层的维度 \(d_{ff} = 2048\) 。

9.4.3.4 嵌入和 Softmax

和其它序列转导模型类似，我们使用嵌入层将输入和输出标记转换为维度为 \(d_{model}\) 的向量。我们还使用线性变换和 softmax 函数将解码器输出转换为预测下一个标记的概率。在我们的模型中，两个嵌入层和 softmax 线性变换使用相同的矩阵。在嵌入层，我们将权重乘以 \(\sqrt{d_model}\) 。

9.4.3.5 位置编码

因为我们的模型不包含循环和卷积操作，为了让模型利用序列的顺序信息，我们必须注入以下有个序列中标记的相对或绝对位置的信息。

为此，我们在编码器和解码器堆栈底部的输入嵌入中添加了位置编码，位置编码具有与嵌入相同的维度 \(d_{model}\) ，因此它们可以直接相加，位置编码有很多种选择。

在本工作中，我们使用不同频率的正弦和余弦函数：

                \(PE_{(pos, 2i)} = sin(pos / 10000^{2i/d_{model}})\) 
 \(PE_{(pos, 2i+1)} = cos(pos / 10000^{2i/d_{model}})\) 
            

其中 \(pos\) 是位置，\(i\) 是维度。也就是说，位置编码的每个维度都对应一个正弦曲线。波长从 \(2\pi\) 到 \(10000 \dot 2\pi\) 呈几何级数。

我们之所以选择这个函数，是因为我们假设它可以允许模型轻松地通过相对位置来学习关注，因为对于任何固定偏移量 \(k\) ，\(PE_{pos+k}\) 可以被表示成 \(PE_{pos}\) 的线性函数。

我们还尝试了可学习的位置嵌入，发现两个版本产生的结果几乎相同。选择正弦版本，是因为它可能允许模型推断出比训练期间遇到的序列长度更长的序列长度。

9.4.4 自注意力？

在本小节中，我们将自注意力的各个方面与循环层和卷积层进行比较。他们常用于将一个变长序列表示 \(x_1, ... , x_n\) 映射称为另外一个序列 \(z_1, ... , z_n\) ，其中 \(x_i, z_i \in \mathbb{R}^d\) ，像是典型序列转换编码器或者解码器中的隐藏层。激励我们使用自注意力的有 3 个考量。

一个是每层的总计算复杂度。另一个是可以并行化，需要很少的序列操作。

第三个是网络的长距离依赖。学习长距离依赖是许多序列转导任务中的关键挑战。影响学习此类依赖关系能力的一个关键因素是前向和反向信号在网络中必须经过的路径的长度。输入和输出序列中任何位置组合之间的路径越短，学习长程依赖关系就越容易。因此，我们还比较了由不同层类型组成的网络中任意两个输入和输出位置之间的最大路径长度。

如下表所示，自注意力层用恒定数量的连续操作连接所有位置，而循环层则需要 \(O(n)\) 个连续操作。在计算复杂度方面，当序列长度 \(n\) 小于表示维数 \(d\) 时，自注意力层比循环层更快，这在机器翻译中最先进的模型使用的句子表示中最常见，例如单词片段和字节对表示。为了提高涉及非常长序列的任务的计算性能，可以将自注意力限制为仅考虑以相应输出位置为中心的输入序列中大小为 r 的邻域。这会将最大路径长度增加到 \(O(n/r)\)。我们计划在未来的工作中进一步研究这种方法。

单个卷积核（核宽度 \(k < n\) 不会连接所有输入和输出位置对。如果使用连续核，则需要堆叠 \(O(n/k)\) 个卷积层；如果使用扩张卷积，则需要堆叠 \(O(logk(n))\) ，从而增加网络中任意两个位置之间最长路径的长度。卷积层通常比循环层更贵，大约是 \(k\) 倍。然而，可分离卷积可显著降低复杂度，降至 \(O(k \dot n \dot d + n \dot d^2)\) 。即使 \(k = n\) ，可分离卷积的复杂度也等于自注意力层和前馈层，这是我们在模型中采用的方法。

作为附带好处，自注意力可以产生更多可解释的模型。我们检查模型中的注意力分布，并在附录中展示和讨论示例。不仅单个注意力头清楚地学会了执行不同的任务，而且学多注意力似乎表现出与句子的句法和语义结构相关的行为。

9.4.5 训练

本小节描述了我们模型的训练方案。

9.4.5.1 训练数据和小批量

我们对包含约 450 万个句子对的标准 WMT 2014 英语-德语数据集进行了训练。使用 字节对编码 (Byte-pair Encoding) 对句子进行编码，该编码包含源词汇和目标词汇总共 37000 个标记。

对于英语-法语，我们使用了更大的 WMT 2014 英语-法语数据集，该数据集包含 3600 万个句子，并将标记拆分为 32000 个单词的词汇表。句子按照近似长度进行分批。每个训练批次包含一组局子对，其中包含大约 25000 个源标记和 25000 个目标标记。

9.4.5.2 硬件和日程

我们在一台配备 8 个 NVIDIA P100 GPU 的机器上训练了我们的模型。对于使用本文所述超参数的基础模型，每个训练步骤大约需要 0.4 秒。我们训练了基础模型总共 100,000 步或 12 小时。对于我们的大模型（在表 3 的底部描述），步骤时间为 1.0 秒。大模型训练了 300,000 步（3.5 天）。

9.4.5.3 优化器

我们使用 Adam 优化器，它的参数为 \(\beta_1 = 0.9\) ，\(\beta_2 = 0.98\) 以及 \(\epsilon = 10^{-9}\) 。我们根据以下公式在训练过程中改变学习率：

                \(lrate = d_{model}^{-0.5} \dot min(step\_num^{-0.5} , step\_num \dot warmup\_steps^{-1.5})\)
            

这相当于在第一个 \(warmup_steps\) 训练步骤中线性增加学习率，然后按步数的平方根倒数比例降低。我们使用了 \(warmup_steps = 4000\) 。

9.4.5.4 正则化

训练过程中，我们引入了三种正则化：

残差失活 我们将失活应用于每个子层的输出，然后将其添加到子层输入并进行归一化。此外，我们将失活应用于编码器和解码器堆栈中的嵌入和位置编码的总和。对于基础模型，我们使用的失活率为 \(P_{drop} = 0.1\) 。

标签平滑 在训练期间，我们采用了值为 \(\epsilon_{ls} = 0.1\) 。这会增加困惑度，因为模型学会到更多的不确定性，但会提高准确率和 BLEU 分数。

9.4.6 结果

9.4.6.1 机器翻译

在 WMT 2014 英德翻译任务中，大型 Transformer 模型（表 2 中的 Transformer (big)）的表现比之前报道的最佳模型（包括集成）高出 2.0 BLEU，创下了 28.4 的最新 BLEU 得分。此模型的配置列在表 3 的底部。在 8 个 P100 GPU 上训练耗时 3.5 天。即使是我们的基础模型也超越了所有之前发布的模型和集成，而训练成本仅为任何竞争模型的一小部分。

9.4.6.2 模型变体

为了评估 Transformer 不同组件的重要性，我们以不同的方式改变了基础模型，测量了开发集 newstest2013 上英语到德语翻译的性能变化。我们使用了上一节中描述的波束搜索，但没有使用检查点平均。我们在表 3 中展示了这些结果。

9.4.6.3 英语成分分析

为了评估 Transformer 是否可以推广到其他任务，我们对英语成分解析进行了实验。这项任务提出了特定的挑战：输出受到强大的结构约束，并且比输入长得多。此外，RNN 序列到序列模型在小数据范围内无法获得最先进的结果。

9.4.7 总结

在这项工作中，我们提出了 Transformer，这是第一个完全基于注意力的序列传导模型，用多头自注意力取代了编码器-解码器架构中最常用的循环层。

对于翻译任务，Transformer 的训练速度比基于循环或卷积层的架构快得多。在 WMT 2014 英语到德语和 WMT 2014 英语到法语的翻译任务中，我们达到了最先进的水平。对于前一个任务，我们最好的模型比之前所有的集成模型都要优秀。

我们对基于注意力的模型的未来感到兴奋，并计划将它们应用于其它任务。我们计划将 Transformer 扩展到涉及文本以外的输入和输出模式的问题，并研究局部、受限的注意力机制，以有效处理图像、音频和视频等大量输入和输出。让生成不那么连续是我们的另一个研究目标。

我们用来训练和评估模型的代码可在 https://github.com/google/trax 上找到。

我们感谢 Nal Kalchbrenner 和 Stephan Gouws 的有益评论、更正和启发。