扩散模型的数学基础

11.1 扩散模型的数学基础

理解扩散 (Diffusion) 与逆扩散 (Reverse Diffusion) 的数学原理！

创建日期: 2025-02-16

扩散生成模型 (Diffusion Generative Model) 是一种从分布中生成样本的方法；它与其它方法（如生成对抗网络 (GAN) 和变分自动编码器 (VAE) 有很大不同。值得注意的是，它是 OpenAI 最近的 DALL·E 2 系统的核心元素之一，该系统用于将自然语言描述转换为详细图像。

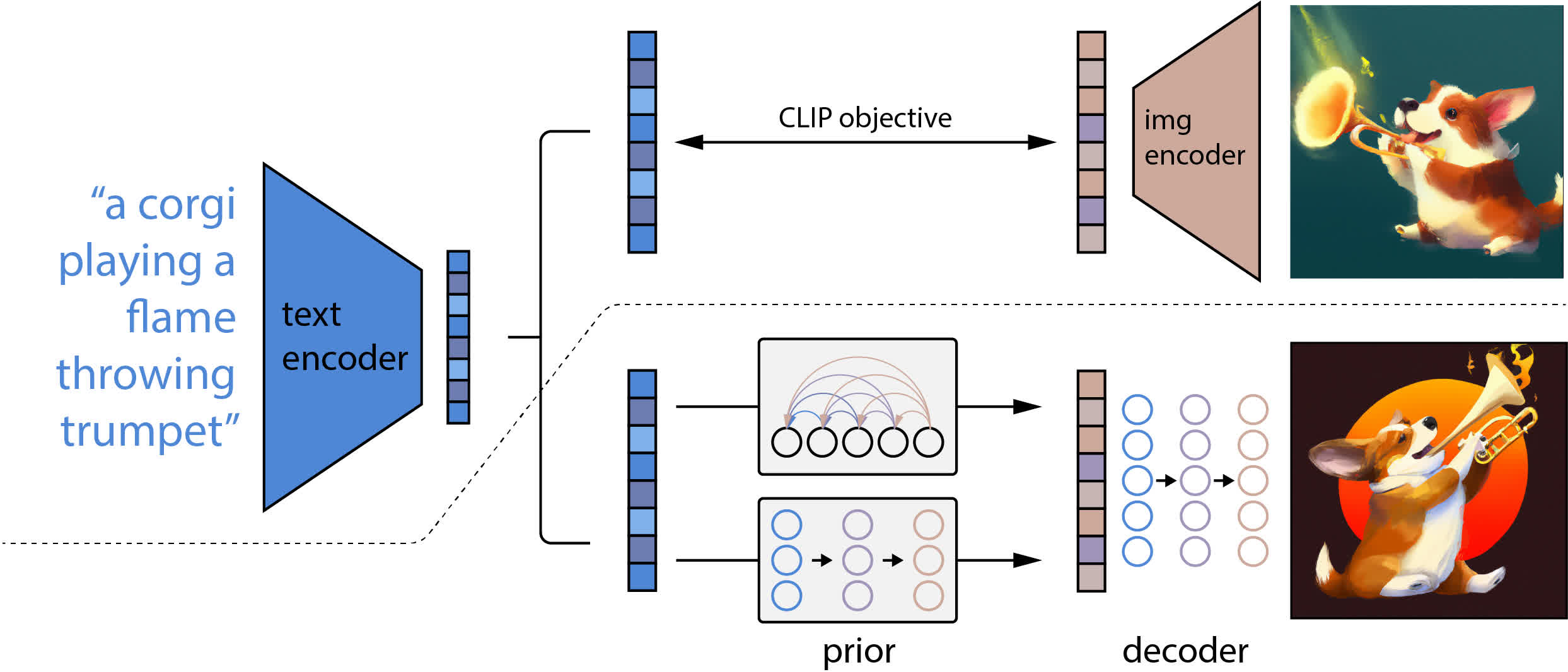
扩散生成模型使用如下思想：来自某些分布（例如图像）的样本逐渐受到越来越多的噪声的破坏，直到它们变得无法识别 - 这就是 扩散 (Diffusion) 。然后我们反转这一过程，以便我们可以将无法识别的图片变成我们感兴趣的分布的样本。因为很容易对无法识别的图片进行采样，所以映射使我们能够轻松地从目标分布中进行采样。

我们将重点关注扩散生成模型的基础，并且主要使用简单的示例用于分析。

11.1.1 动机

生成模型是统计学和机器学习的一个领域，涉及从给定的数据集采样的概率分布。通过学习这样的分布（例如人脸图片），我们可以从中采样新的数据 - 例如一张新的人脸图像。

生成建模有不同的方法，包括使用生成对抗网络 (GAN) 和变分自动编码器 (VAE) 。一种较新的方法是向样本添加大量噪声，然后学习消除噪声。通过这种方式，我们可以学习将纯噪声转换为我们感兴趣的某个分布的样本。因为生成各种纯噪声岩本很容易，而且每个样本都通过我们的噪声消除映射转换为目标分布的样本，所以我们有一个生成模型。

这种生成建模的方法有各种吸引人的特点，其中一个值得注意的特点是，我们不必直接学习概率分布，而是可以学习一个有时称为 得分 (Score) ，下面是对数概率密度函数相对于 \(x\) 的梯度：

\(s(x) := \nabla_xlogp(x)\)

这样我们就避免了必须学习概率密度的标准化常数，它通常是一项麻烦的任务。

我们可以用基于扩散的生成模型做什么？以下是一些常见的事情：

类别生成（给定一个类别标签，生成一个新的样本）；
修复（填补部分损坏图像的缺失部分）；
着色（为灰度图像添加合理的颜色）。

11.1.2 正向扩散和随机过程

我们如何适当地向分布样本添加噪声？尽快对此的看法各不相同，但最近的研究已经统一了不同的方法。总的来说，关于如何做到这一点的，各种想法都相当于对给定的分布样本进行某种扩散过程。更一般地说，我们可以想象将某种随机过程（由随机微分方程或 SDE 定义）应用于分布样本。

11.1.2.1 扩散基础知识

让我们看一下扩散的基础知识，一维扩散过程（在实线上）可以用 随机微分方程 (Stochastic Differential Equation, SDE) 来定义：

\(\dot{x} = \sigma \cdot \eta(t)\)

其中 \(\sigma > 0 \) 是常数，\(\eta(t)\) 表示高斯白噪声。

注：\(\dot{x}\) 表示的是 \(x\) 的导数。

注：高斯函数表达式 \(f(x) = A e^{-\frac{(x - \mu)^2}{2\sigma^2}}\) ，其中 \(\mu\) 是均值，\(\sigma\) 是标准差。

为了计算并通过数据说明上述方程，我们可以使用数值方法对其进行模拟。假设 \(\sigma = 2\) ，并且 \(\eta(t)\) 是一个标准的高斯白噪声。那么计算步骤如下：

设定初始条件，比如 \(x(0) = 0\) ；
使用离散时间步长（例如 \(\Delta{t} = 0.01\) ），模拟 \(x(t)\) 在时间 \(t\) 上的变化；
生成每个时间步的高斯白噪声增量 \(\eta(t)\) ；
计算每个时间步的变化 \(\dot{x}(t) = \sigma \cdot \eta(t)\) ；
更新 \(x(t)\) 的值：\(x(t + \Delta{t}) = x(t) + \dot{x}(t)\Delta{t}\) 。

使用 Python 进行模拟，代码在文件中：

import numpy
from matplotlib import pyplot

sigma = 2
duration = 10
dt = 0.01
num = int(duration / dt)

t = numpy.linspace(0, duration, num)
x = numpy.zeros(num)

rng = numpy.random.default_rng(0)
eta = rng.standard_normal(num)

for i in range(1, num):
    dot_x = sigma * eta[i]
    x[i] = x[i-1] + dot_x * dt

pyplot.plot(t, x)
pyplot.title('Simulated System with Gaussian White Noise')
pyplot.xlabel('Time (t)')
pyplot.ylabel('x(t)')
pyplot.grid(True)
pyplot.subplots_adjust(top=0.92, right=0.92)
pyplot.show()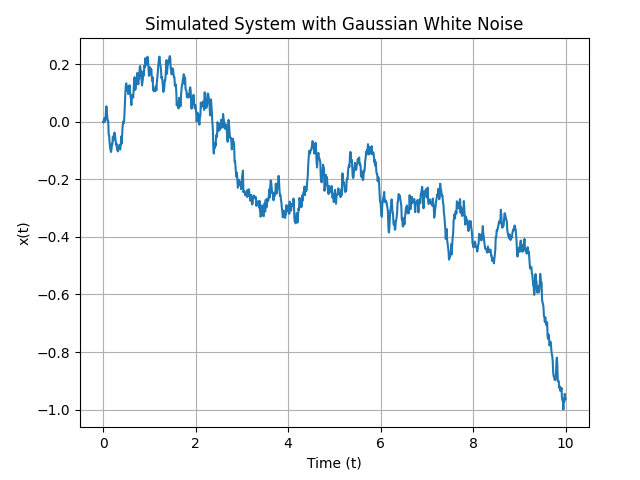

这到底是什么意思呢？我们可以将上述表达式具体化，定义一个很小的离散增量 \(\Delta{t}\) ：

\(x(t + \Delta{t}) = x(t) + \sigma\sqrt{\Delta{t}} \cdot r\)

其中 \(r \sim \mathcal{N}(0, 1)\) 是标准正态分布的样本。Euler-Maruyama 是个很好的示例，Euler-Maruyama 方法是数值解随机微分方程的一种显示欧拉方法。它是标准欧拉方法在随机过程下的推广，用于求解具有布朗运动或噪声项的微分方程。标准形式的 SDE 为：

\(dX_t = f(X_t, t)dt + g(X_t, t)dW_t\)

其中 \(X_t\) 是随机过程，\(f(X_t, t)\) 是漂移项，表示系统确定性部分，\(g(X_t, t)\) 是扩散项，表示噪声的影响，\(W_t\) 是布朗运动。给定时间步长 \(\Delta{t}\) ， Euler-Maruyama 方法的离散化形式为：

\(X_{n+1} = X_n + f(X_n, t_n)\Delta{t} + g(X_n, t_n)\Delta{W_n}\)

\(f(X_n, t_n)\) 近似表示在时间步 \(t_n\) 系统的变化率。

上述扩散描述对于模拟很有用。给定一个数字 \(x\) ，我们可以使用上述更新规则使其经过一个时间步的扩散。但是互补的观点描述概率密度 \(p(x, t)\) ，系统在 \(t\) 时刻 \(x\) 位置的概率，随着时间而变化。

尤其是 \(p(x, t)\) 随着著名的扩散等式变化：

                \(\frac{\partial{p(x, t)}}{\partial{t}} = \frac{\sigma^2}{2} \cdot \frac{\partial^{2}p(x, t)}{\partial{x^2}}\)
            

你可能习惯于看到这个方程具有扩散常数 \(D\) 而不是参数 \(\sigma\) ，它们之间的转换关系为 \(D := \frac{\sigma^2}{2}\) 。

给定 \(\delta\) 函数初始条件 \(p(x, 0) = \delta(x - x_0)\) （也就是说系统在初始 \(x_0\) 位置），那么扩散方程的通解为：

                \(p(x, t|x_0, 0) = \frac{1}{\sqrt{2\pi\sigma^{2}t}} exp \{-\frac{(x - x_0)^2}{2\sigma^{2}t}\}\)
            

给定任意初始条件 \(p(x, 0) = p_{0}(x)\) ，扩散函数的通解是：

\(p(x, t) = \int_{-\infty}^{\infty}p(x, t|x_0, 0)p_0(x_0)dx_0\)

11.1.2.2 随机微分方程基础

扩散只是由随机微分方程控制的随机过程的一个特别简单的例子。最一般的随机微分方程如下所示：

\(\dot{x} = f(x, t) + g(x, t)\eta(t)\)

其中 \(f(x, t)\) 和 \(g(x, t)\) 是函数，\(\eta(t)\) 是高斯白噪声。函数 \(f(x,t )\) 是漂移项，描述了 \(x(t)\) 随时间的变化。\(g(x, t)\) 是噪声或者扩散项，描述 \(x(t)\) 的随机波动。

它意味着什么？不像扩散那样，\(g(x, t)\) 是常数，使上述表达式定义明确还需要一些其它数学知识。为了我们的目的，选择限免的公式进行描述：

\(x(t + \Delta{t}) = x(t) + f(x(t), t)\Delta{t} + g(x, t)\sqrt{\Delta{t}}r\)

\(r \sim \mathcal{N}(0, 1)\) 是标准正态分布的样本。这是更通用的 Euler-Maruyama 方法（尽管考虑到我们目前只在一维上工作，它仍然不是最通用的形式），

扩散方程的类似方程是 Fokker-Planck 等式，它描述了 \(p(x, t)\) 在随机微分方程下随时间的变化。其表达式可以写成：

                \(\frac{\partial{p(x, t)}}{\partial{t}} = -\frac{\partial}{\partial{x}}[f(x, t)p(x, t)] + \frac{\partial^2}{\partial{x^2}}[\frac{{g(x, t)^2}}{2}p(x, t)]\)
            

绝大多数 Fokker-Planck 等式都非常难解决，因此我们无法获得 \(p(x, t)\) 准确的解。我们可以解决的 \(p(x, t)\) 只包含扩散，和 Ornstein-Uhlenbeck-like 过程，该过程使反向随机过程，以下是一维的示例：

\(\dot{x} = \frac{1}{\tau}[\mu - x] + \sigma\sqrt{frac{2}{\tau}}\eta(t)\)

对于初始条件 \(p(x, 0) = \delta(x - x_0)\) ，它的解为：

                \(p(x, t|x_0, 0) = \frac{1}{\sqrt{2\pi{s}{t}^2}}exp\{-\frac{[x - \mu(t)]^2}{2st^2}\}\)
            

其中：

                \(u(t) := x_0e^{-t/r} + \mu(1 - e^{-t/\tau})\) 
 \(s(t)^2 := \sigma^2(1 - e^{-2t/\tau})\)
            

通用的 Ornstein-Uhlenbeck-like 解决方法（初始分布 \(p(x, 0) = p_0(x)\)）：

\(p(x, t) = \int_{-\infty}^{\infty} p(x,t|x_0, 0)p_0(x_0) \, dx_0\)

Ornstein-Uhlenbeck 过程与严格扩散过程不同之处在于，Ornstein-Uhlenbeck 过程的长期行为会丢失所有关于其初始条件的记忆。也就是说，随着 \(t\) 时间的增加，\(p(x, t)\) 越来越不依赖 \(p_0(x)\) 。

扩散过程：没有回归到某个平衡值得趋势，状态得变化完全依赖于随机噪声。OU 过程：具有回归到均值得趋势，状态变化不仅受随机扰动影响，还有回归到某个平衡点得力量。

11.1.2.3 基础示例

让我们看看模拟一维扩散（一种特别简单的随机过程）会是什么样子。也可以使用代码来模拟其它 SDE，例如 OU 过程，具体实现在文件里。

以下是一些实用函数，前几个函数用于正向模拟 1D 扩散（尽管 forward_SDE_simulation 可用于模拟更通用的 SDE ）。

11.1.2.4 通用 SDE

\(\dot(x) = f(x, t) + g(x, t)\eta(t)\)

11.1.3 逆扩散

我们如何消除在正向扩散过程中添加到样本中的噪声？虽然这有点违背直觉 -- 例如我们期望观察到奶油和咖啡通过扩散混合，但不希望它们自发分离 -- 但事实证明，由 SDE 控制的随机过程的时间反转在数学上是很简单的事。时间反转过程本身就是由 SDE 控制的随机过程，器概率密度根据 Fokker-Planck 方程随时间演变。

11.1.3.1 反向 1D 扩散

回想一下，一维扩散（持续一段时间 \(T\) ）可以用 SDE 描述：

\(\dot(x) = \sigma \dot \eta(t)\)

直观上看，扩散会导致物质散开。我们预计，这一过程的时间逆转会导致物质重新聚集在一起。

一个随机过程是 OU 过程，它将事物集中起来，而不是将它们分散开来。某种 OU 过程可能是 1D 扩散的时间反转吗？事实证明，由以下公式描述的 OU 过程：

\(\dot(x) = \frac{x_0 - x}{T - t} + \sigma \dot \eta(t)\)

是开始于点 \(x_0\) ，经过时间 \(T\) 的扩散过程的时间逆转。换句话说，这个过程压缩了高斯函数，直到它变成时间 \(T\) 的中心点在 \(x_0\) 。

转移概率也反转：

请注意，我们使用的是时间向前运行的惯例，从 \(t = 0\) 到 \(t = T\) 。这里，需要将时间反转过来，从 \(t = T\) 到 \(t = 0\) ，那么有以下的公式：

                \(x(t - \Delta{t}) = x(t) - \frac{(x_0 - x)}{t}\Delta{t} + \sigma \sqrt{\Delta{t}}r\)
            

11.1.3.2 通用反向随机过程

是否有一些系统的方法来推导逆过程？幸运的是：

\(\dot(x) = f(x, t) + g(t)\eta(t)\)

\(q(x, t) = p(x, T - t)\)

11.1.3.3 得分函数

上述表达式的逆过程包含一个看起来很有趣的函数：得分函数，如下定义：

\(s(x, t) := \nabla_{x}p(x, t)\)

表示在 \(t\) 时刻，概率密度函数 \(p(x, t)\) 关于空间位置 \(x\) 的梯度。

如果我们想对某些噪声进行逆过程，并将其转换为目标分布中的样本，我们需要知道得分函数，这实际上是整个生成建模方法的关键难点。

为什么这很难？我们不知道 \(p(x, t)\) ！如果我们知道，就可以直接从中取样，而不是进行逆扩散。

虽然这看起来像是先有鸡还是先有蛋的问题，但情况并没有看起来那么糟糕。我们确实需要学习得分函数，比直接学习 \(p(x, t)\) 容易，我们还需要学习一个标准化因子（这很难）。

11.1.3.4 得分函数示例

从质量点的 1D 扩散

考虑具有 \delta 函数的一维扩散情况，时间相关概率为：

                \(p(x, t) = \frac{1}{\sqrt{2\pi\sigma^{2}t}}exp\{-\frac{(x-x_0)^2}{2\sigma^2t}\}\)
            

它的得分函数是：

\(s(x, t) = \frac{\partial}{x}logp(x, t) = -\frac{(x - x_0)}{\sigma^2t}\)

11.1.3.5 基础示例代码

11.1.4 学习得分函数

现在让我们尝试真正解决先有鸡还是先有蛋的问题，我们希望通过反向扩散从某个目标分布（其函数形式未知，并且我们只能通过样本访问）中进行采样，但这样做需要我们知道与目标分布相对应的得分函数。知道得分函数（该分布对数的梯度）似乎等同于知道分布本身。我们如何学习得分函数？

首先，让我们写下一个合理的目标函数。假设我们有一个参数化的得分函数 \(s_{\theta}(x, t)\) ，它依赖于一系列的参数 \(\theta\) 。对于所有的 \(x\) 和 \(t\) ，我们希望尽可能近似，所以有如下公式：

                \(J(\theta) :\stackrel{?}{=} \frac{1}{2}\int dxdt[s_{\theta}(x, t) - \Delta_xlogp(x, t)]^2\)
            

上面的目标函数有个问题就是没有考虑有特定的 \(x\) 比其它更有价值。我们特别感兴趣的是让得分函数对哪些可能性很高的值计算正确，因此对上述内容进行合理的修改：

                \(J(\theta) :\stackrel{?}{=} \frac{1}{2}\int dxdtp(x, t)[s_{\theta}(x, t) - \Delta_xlogp(x, t)]^2\)
            

类似的，我们可以考虑添加一个随着时间而变化的加权因子，因为与精确得分函数的偏差尺度会随着时间而改变：

                \(J_{naive}(\theta) :\stackrel{?}{=} \frac{1}{2}\int dxdt\lambda(t)p(x, t)[s_{\theta}(x, t) - \Delta_xlogp(x, t)]^2\)
            

这是一个非常合理的目标函数。但我们有一个重大的问题：就是很难估计 \(p(x,t)\) 的梯度，因为 \(p(x, t)\) 可能强烈依赖于 \(p(x, 0)\) （比如目标分布）。我们不知道目标分支，这就是我们做着一切的原因。

此时，我们可以使用一个有趣的技巧。尽管上述目标函数非常合理，但很难使用；技巧是找到具有相同全局最小值的代替目标函数。事实证明，可以通过以下公式提供：

11.1.4.1 定义目标函数

11.1.4.2 使用样本逼近

转移概率对数的梯度为：

\(\Delta_xlogp(x, t|x^{(0)}, 0) = - \frac{[x - x^{(0)}]}{\sigma^2(t)}\)

现在我们可以近似地评估损失函数，可以让计算机处理梯度...剩下的是计算时间！

11.1.4.3 神经网络逼近

现在我们有了一个定义明确的优化问题，以及一个解决该问题的简单方法，我们开业i利用各种工具来解决这个问题。由于我们需要构建得分函数的一些参数化近似值，（深度）神经网络就是这样一种工具。

转向神经网络并不需要对我们上面概述的图景进行任何实质性的概念改变。我们将会在下一个小节看到，一旦其它一切都设置好，将神经网络作为得分函数近似器实际上就非常简单！