9.1 注意力机制
注意力机制 (Attention Mechanism) !
创建日期: 2025-01-18
注意力机制 (Attention Mechanism) 是一种机器学习技术,它指导深度学习模型优先考虑(或关注)输入数据中最相关的部分。注意力机制的创新促成了 Transformer 架构的诞生,该架构催生了 现代大语言模型 (Large Language Model, LLM) ,为 ChatGPT 等热门应用程序提供支持。
9.1.1 历史发展
顾名思义,注意力机制的灵感来源于人类(和其它动物)选择性地关注突出细节并忽略当前不太重要的细节的能力。获取所有信息但只关注最相关的信息有助于确保不会丢失任何有意义的细节,同时还能有效利用有限的内存和时间。举个例子,用一句话描述下图:

大部分的人都会说“一只鸭子在水里游”,可以看到这里我们忽略了青山,我们的大脑经过不断地学习,第一反应是将注意力放在鸭子身上。
在心理学中,注意力(Attention)是指人类大脑对特定信息的优先选择和处理的能力,是认知心理学的核心研究领域之一。注意力不仅影响我们的感知、记忆和决策,还涉及多种行为任务的完成。
从数学上讲,注意力机制计算 注意力权重 (Attention Weight) ,该权重反映了输入序列的每个部分对当前任务的相对重要性。然后,它根据输入序列每个部分的重要性,应用这些注意力权重来增加(或减少)输入序列每个部分的影响。注意力模型(即采用注意力机制的人工智能模型)通过对大量示例进行监督学习或自我监督学习来训练,以分配准确的注意力权重。
输入 "It is in this spirit that a majority of American governments have passed new laws since 2009 making the registration or voting process more difficult.",下图是注意力权重的可视化:
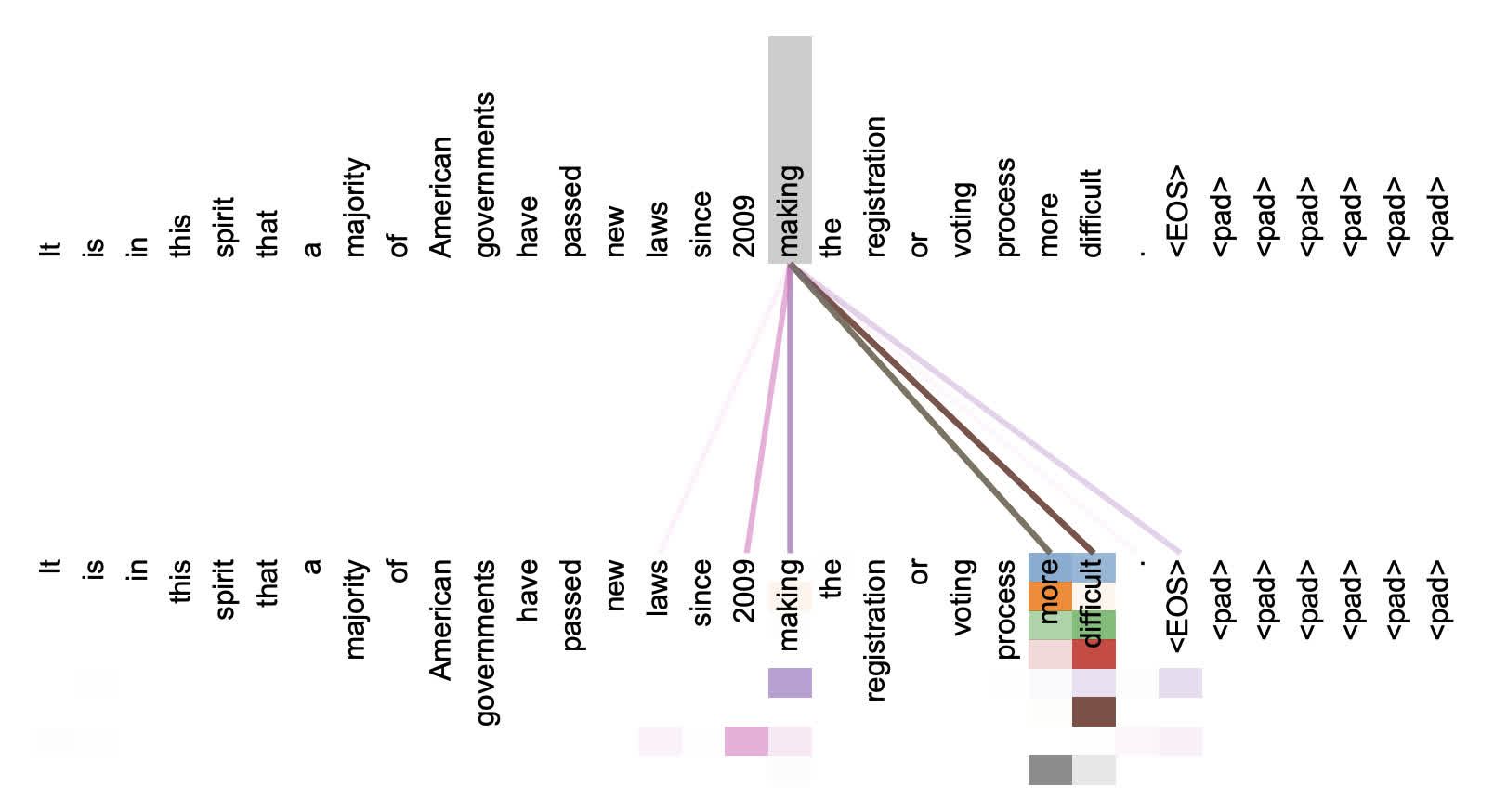
许多注意力头(不同颜色代表不同的注意力头)关注动词 "making" 的远距离关系,从而完成短语 "making ... more difficult" ,此处仅显示针对单词 "making" 的注意力。
注意力机制最初由 Bahdanau 等人于 2014 年提出(论文 Neural Machine Translation by Jointly Learning to Align and Translate),作为一种技术来解决当时用于机器翻译的最先进的循环神经网络 (RNN) 模型的缺点。后续研究将注意力机制整合到用于图像字幕和视觉问答等任务的卷积神经网络 (CNN) 中。
2017 年,开创性的论文 Attention Is All You Need 引入了 Transformer 模型,该模型完全摒弃了循环和卷积,只采用注意力层和标准前馈层。从那时起,Transformer 架构就成为了推动生成式 AI 时代发展的尖端模型的支柱。
虽然注意力机制主要与用于自然语言处理 (NLP) 任务(例如摘要、问答、文本生成和情感分析),但基于注意力的模型也广泛应用于其他领域,先进的图像生成扩散模型通常包含注意力机制。
了解了注意力机制的历史,接下来通过代码理解注意力在计算机中是如何实现!
9.1.2 注意力提示
注意力是如何应用于视觉世界中的呢?这要从当今十分普及的双组件框架说起,这个框架的出现可以追溯到 19 世纪 90 年代的美国信息学之父威廉·詹姆斯,他是当时最具影响力的心理学家和哲学家之一,在其著作《心理学原理》中,将注意分为主动注意和被动注意:
-
1. 被动注意 (Passive Attention)
定义:被动注意是指我们的注意力不由自主地被外界刺激所吸引,而将注意力集中在它上面。这种注意力通常是无意识的,不需要付出努力。
- 听到巨大的声响而转头去看;
- 被色彩鲜艳的广告牌所吸引;
- 在人群中突然听到自己的名字;
- 看到移动的物体;
- 闻到香味。
越响、越亮、越鲜艳的刺激越容易引起被动注意。
-
2. 主动注意 (Active Attention)
定义:主动注意是指有意识地、主动地将注意力集中在某个事物或任务上,这种注意是有目的的,需要付出努力和意志力。
- 在嘈杂的环境中专心阅读一本书;
- 在会议上集中精力听取发言人讲话;
- 为了完成工作而集中精力处理文件;
- 学习新的技能;
- 解决复杂的问题。
倾向于关注自己感兴趣或与目标相关的事物。
在日常生活中,主动注意和被动注意并不是完全独立的,它们经常相互作用。例如,我们可能主动选择去听一场音乐会(主动注意),但在音乐会中,我们可能会被美妙的旋律或歌手的表演所吸引(被动注意)。
9.1.3 查询、键和值
在计算机科学的注意力机制中,查询 (Query) 、键 (Key) 和 值 (value) 的核心思想是模仿人类的注意力机制来动态选择重要信息。具体含义如下:
-
1. 查询 (Query)
表示我们想要寻找什么或关注什么,类似于心理学中主动注意的目标,是由任务需求驱动的。
-
2. 键 (Key)
表示数据中的潜在目标,是系统要扫描的对象特征,类似于心理学中被动注意机制的外部刺激。
-
3. 值 (Value)
表示与某个键相关联的内容或信息,类似于心理学中关注后的实际信息提取。
主动注意对应的是 Query 的作用——明确地表示“我要寻找什么”,例如在阅读文章时,主动注意会将注意力集中在与目标(Query)相关的关键词(Key)上,提取对应的值(Value)。
被动注意对应的是 Key 的显著性作用——环境中的某些刺激自动吸引注意。被动注意的触发依赖于键值对的匹配。当一个人分心时,环境中的突发噪音(Key)触发了无意识的注意力转移,导致人关注这个刺激,并提取相应的信息(Value)。
主动注意与被动注意解释了人类的注意力方式,下面来看看如何通过这两个注意力,用神经网络来设计注意力机制的框架。
首先,考虑一个相对简单情况,即只使用被动注意。要想将选择偏向于感官输入,则可以简单地使用参数化的全连接层,甚至是非参数化的最大汇聚层或 平均汇聚层 。
因此,是否包含主动注意将注意力机制与全连接层或汇聚层区别开来。在注意力机制的背景下,主动注意被称为查询。给定任何查询,注意力机制通过 注意力汇聚 (Attention Pooling) 将选择引导至感官输入中,它们被称为值 (Value) 。
更通俗的解释是,每个值 (Value) 都与一个键 (Key) 匹配,这可以理解成感官的被动注意,如下图所示,可以通过设计注意力汇聚的方式,便于给定的查询与键进行匹配,这将引导得到最匹配的值(感官输入):
9.1.4 注意力汇聚
查询(主动注意)和键(被动注意)之间的交互形成了注意力汇聚,注意力汇聚有选择地聚合了值(感官输入)以生成最终的输出。接下来介绍注意力汇聚的更多细节,以便从宏观上了解注意力机制在实践中的运作方式。
具体来说,1964 年提出的 Nadaraya-Watson 核回归模型 是一个简单但完整的例子,可以用于演示具有注意力机制的机器学习。
9.1.4.1 生成数据集
简单起见,考虑下面的回归问题:给定成对的(输入-输出)数据集 \(\lbrace(x_1, y_1), ... , (x_n, y_n)\rbrace\) ,如何学习 \(f\) 来预测任意新的输入 \(x\) 的输出 \(\hat{y} = f(x)\) ?
根据下面的非线性函数生成一个人工数据集:
\(y_i = 2sin(x_i) + x_i^{0.8} + ξ\)
其中 \(ξ\) 为加入的噪声项,服从均值为 0 和标准差为 0.5 的正态分布。在这里生成了 50 个训练样本。为了更好地可视化,需要对训练样本进行排序,代码在 random_point_dataset.py 文件里:
def func(x):
return 2 * numpy.sin(x) + x**0.8
rng = numpy.random.default_rng(0)
n_train = 50
x_train = numpy.sort(rng.random(n_train) * 5)
y_train = func(x_train) + rng.normal(0.0, 0.5, (n_train,))
x = numpy.arange(0, 5, 0.05)
y_truth = func(x)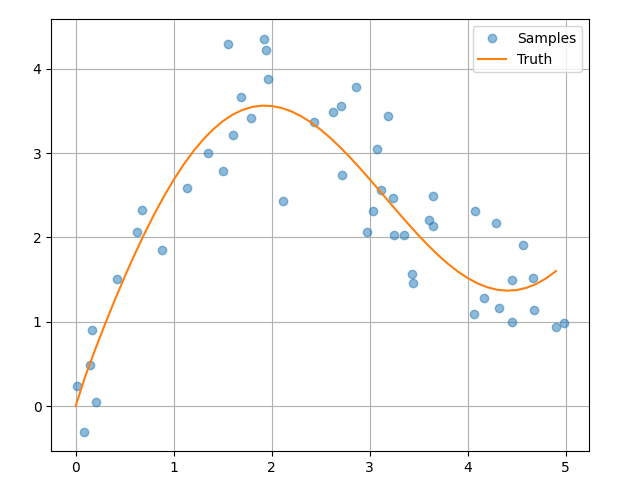
9.1.4.2 平均汇聚
先使用最简单的估计器来解决回归问题,基于平均汇聚来计算所有训练样本输出的平均值:
\(f(x) = \frac{1}{n}\sum_{i=1}^{n} y_i\)
代码实现在 average_pooling.py 文件里,学习得到的预测函数使用 Pred 进行标记:
y_pred = y_train.mean().repeat(len(x))如下图所示,这个估计器确实不够聪明,真实函数 (Truth) 和预测函数 (Pred) 相差很大:
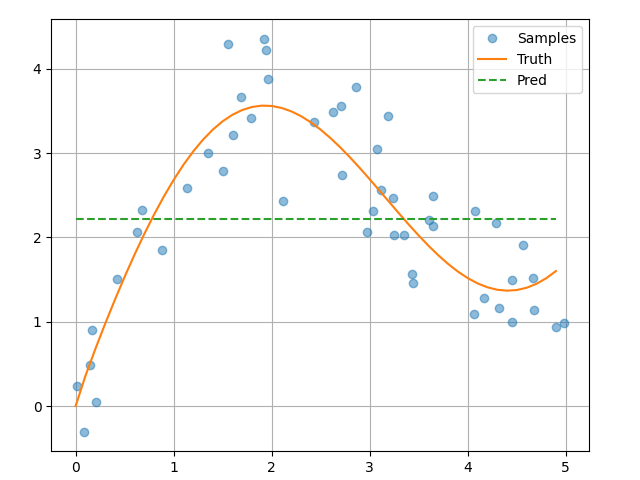
9.1.4.3 无参注意汇聚
显然,平均汇聚忽略了输入 \(x_i\) 。于是 Nadaraya 和 Watson 提出了一个更好的想法,根据输入的位置对输出 \(y_i\) 进行加权:
\(f(x) = \sum_{i=1}^{n} \frac{K(x - x_i)}{\sum_{j=1}^{n} K(x - x_j)} y_i\)
其中 \(K\) 是核 ,上述公式被称为 Nadaraya-Watson 核回归。这里不会深入讨论核函数细节,但受此启发,我们可以得到一个更加通用的注意力汇聚公式:
\(f(x) = \sum_{i=1}^{n} \alpha(x, x_i)y_i\)
其中 \(x\) 是查询,\((x_i, y_i)\) 是键值对,将查询 \(x\) 和键 \(x_i\) 之间的关系建模为注意力权重 \(\alpha(x, x_i)\) ,这个权重将被分配给每一个对应值 \(y_i\) 。对于任何查询,模型在所有键值对的注意力权重都是一个有效的概率分布:它们是非负的,并且总和为 1 。
为了更好地理解注意力汇聚,下面考虑一个 高斯核 (Gaussian Kernel) ,其定义为:
\(K(\mu) = \frac{1}{\sqrt{2\pi}} exp(-\frac{{{\mu}^2}}{2})\)
将高斯核代入注意力汇聚公式可以得到:
给定一个向量 \(z = [z_1, z_2, \dots, z_n]\) ,Softmax 函数将其转换为一个概率分布 \(p = [p_1, p_2, \dots, p_n]\) ,其中每个 \(p_i\) 对应于输入向量 \(z\) 中的元素 \(z_i\) 的归一化概率,公式如下:
上面公式表明,如果一个键 \(x_i\) 越是接近给定的查询 \(x\) ,那么分配给这个键对应值 \(y_i\) 的注意力权重就会越大,也就是“获得了更多的注意力”,代码在 nonparam_pooling.py 文件里:
# Each row contains the same input (query).
x_pred_repeat = x.repeat(n_train).reshape((-1, n_train))
# shape: (n_pred, n_train)
attention_weights = torch.nn.functional.softmax(-(torch.tensor(x_pred_repeat - x_train))**2 / 2, dim=1)
print('Attention weigths shape:', attention_weights.shape)
y_hat = torch.matmul(attention_weights, torch.tensor(y_train))注意力权重的维度由预测的次数和训练样本的个数确定:
Attention weigths shape: torch.Size([100, 50])
Nadaray-Waston 核回归是一个无参模型,接下来我们将基于这个模型来绘制预测结果。从绘制的结果会发现新的模型预测是平滑的,比平均汇聚的预测更接近真实。
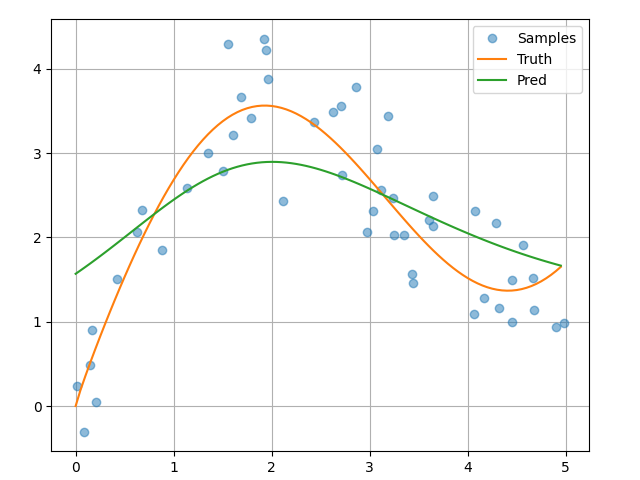
文件 show_heatmap.py 提供了一个绘制热力图的函数,能够可视化注意力权重:
def show_heatmap(matrices, x_label = '', y_label = '', cmap='Reds'):
num_rows, num_cols = matrices.shape[0], matrices.shape[1]
fig, axes = pyplot.subplots(num_rows, num_cols,
sharex=True, sharey=True, squeeze=False)
# shape os axes: (1 x 1)
for row_idx, (row_axes, row_matrices) in enumerate(zip(axes, matrices)):
for col_idx, (ax, matrix) in enumerate(zip(row_axes, row_matrices)):
pcm = ax.imshow(matrix, cmap=cmap)
if row_idx == num_rows - 1:
ax.set_xlabel(x_label)
if col_idx == 0:
ax.set_ylabel(y_label)
fig.colorbar(pcm, ax=axes, shrink=0.6)
fig.subplots_adjust(left=0.1, right=0.96, top=0.96, bottom=0.1, wspace=0.2, hspace=0.2)
pyplot.show()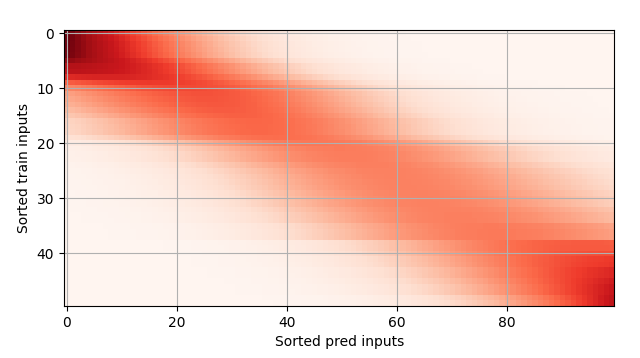
9.1.4.4 有参注意汇聚
无参数的 Nadaraya-Watson 核回归具有一致性的优点:如果有足够的数据,此模型会收敛到最优结果。尽管如此,我们还是可以轻松地将可学习的参数集成到注意力汇聚中。
与无参注意汇聚公式略有不同,在将查询 \(x\) 和键 \(x_i\) 之间的距离乘以可学习参数 \(w\):
为了更有效地计算小批量数据的注意力,我们可以利用批量矩阵乘法。假设第一个小批量数据包括 \(n\) 个矩阵 \(X_1, ... , X_n\) ,矩阵的形状为 \(a \times b\) ,第二个小批量包含 \(n\) 个矩阵 \(Y_1, ... , Yn\) ,矩阵的形状为 \(b \times c\) 。
它们的批量矩阵乘法得到 \(n\) 个矩阵 \(X_{1}Y_1, ... , X_{n}Y_n\) ,形状为 \(a \times c\) 。因此,假定两个张量的形状分别为 \((n, a, b)\) 和 \((n, b, c)\) ,它们的批量矩阵乘法输出的形状为 \((n, a, c)\) ,具体计算过程在 batch_array_dot.py 文件里:
x = torch.ones((2, 1, 4))
y = torch.ones((2, 4, 6))
print(torch.bmm(x, y).shape)torch.Size([2, 1, 6])
在注意力机制的背景中,我们可以使用小批量矩阵乘法来计算小批量数据中的加权平均值:
weights = (torch.ones((2, 10)) * 0.1).unsqueeze(1)
values = torch.arange(20.0).reshape((2, 10)).unsqueeze(-1)
print('Weights shape:', weights.shape)
print('Values shape:', values.shape)
result = torch.bmm(weights, values)
print('Result shape:', result.shape)Weights shape: torch.Size([2, 1, 10]) Values shape: torch.Size([2, 10, 1]) Result shape: torch.Size([2, 1, 1])
基于带参数的注意力汇聚,使用小批量矩阵乘法,定义带参数的 Nadaraya-Watson 核回归版本,代码在 param_pooling.py 文件里:
class NWKernelRegression(torch.nn.Module):
def __init__(self, **kwargs):
super().__init__(**kwargs)
self.w = torch.nn.Parameter(torch.tensor([0.1]), requires_grad=True)
def forward(self, queries, keys, values):
queries = queries.repeat_interleave(keys.shape[1]).reshape((-1, keys.shape[1]))
self.attention_weights = torch.nn.functional.softmax(
-((queries - keys) * self.w) ** 2 / 2, dim=1)
return torch.bmm(self.attention_weights.unsqueeze(1),
values.unsqueeze(-1)).reshape(-1)注:参数 \(w\) 的初始值会很大程度影响最终的结果。
训练带参数的注意力汇聚模型时,使用平方损失和随机梯度下降:
net = NWKernelRegression()
loss = torch.nn.MSELoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=0.5)
for epoch in range(5):
trainer.zero_grad()
l = loss(net(x_train, keys, values), y_train)
l.sum().backward()
trainer.step()
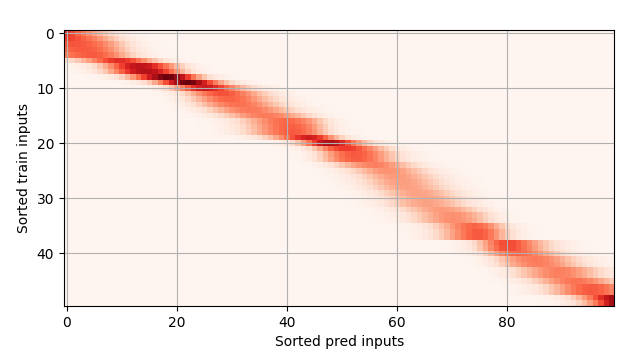
print(f'Epoch {epoch + 1}, loss {float(l.sum().item()):.6f}')如下所示,训练完带参数的注意力汇聚模型后可以发现:在尝试拟合带噪声的训练数据时,预测结果绘制的线不如之前非参数模型的平滑:

为什么新的模型更不平滑呢?下面看一下输出结果的绘制图:与非参数的注意力汇聚模型相比,带参数的模型加入可学习的参数后,曲线在注意力权重较大的区域变得更不平滑:
9.1.5 注意力评分函数
在 9.1.4 小节 中使用了高斯核来对查询核键之间的关系建模,高斯核的指数部分 \(-\frac{1}{2}(x - x_i)^2\) 可以视为 注意力评分函数 (Attention Scoring Function) ,把这个函数的输出结果输入到 softmax 函数中进行计算。通过上述步骤,将得到与键对应的值的概率分布(即注意力权重)。最后,注意力汇聚的输出就是基于这些注意力权重的值的加权和。
从宏观上看,下图实现了注意力机制架构,其中 \(a\) 表示注意力评分函数,由于注意力权重是概率分布,因此加权和其本质上是加权平均值:
用数学语言描述,假设有一个查询 \(q \in R^q\) 和 \(m\) 个键-值对 \((k_1, v_1), ... , (k_m, v_m)\) ,其中 \(k_i \in R^k\) ,\(v_i \in R^v\) 。注意力汇聚函数 \(f\) 就被表示成值的加权和:
其中查询 \(q\) 和键 \(k_i\) 的注意力权重,是通过注意力评分函数 \(a\) 将两个向量映射成标量,再经过 softmax 运算得到的:
正如上图所示,选择不同的注意力评分函数 \(a\) 会导致不同的注意力汇聚操作,本节将介绍两种流行的评分函数,稍后将它们来实现更复杂的注意力模型。
9.1.5.1 掩码 softmax 操作
注意力机制最流行的应用之一是序列模型。因此我们需要能够处理不同长度的序列。在某些情况下,这样的序列可能会出现在同一个小批量中,因此需要使用虚拟标记填充较短的序列。这些特殊标记不具有任何意义。例如,假设我们有以下三个句子:
Dive into Deep Learning Learn to code <blank> Hello world <blank> <blank>
为了仅将有意义的词元作为值来获取注意力汇聚, 可以指定一个有效序列长度(即词元的个数), 以便在计算 softmax 时过滤掉超出指定范围的位置。下面 masked_softmax 函数实现了这样的 掩码 softmax 操作 (Masked Softmax Operation) ,其中任何超出长度的位置都被置为 0 ,代码在 masked_softmax.py 文件里:
def sequence_mask(x, valid_len, value=0):
# Perform softmax operation by masking elements on the last axis.
maxlen = x.size(1)
mask = torch.arange((maxlen), dtype=torch.float32)[None, :] < valid_len[:, None]
x[~mask] = value
return x
def masked_softmax(x, valid_lens):
# Perform softmax operation by masking elements on the last axis.
# x is 3D
if valid_lens is None:
return torch.nn.functional.softmax(x, dim=-1)
else:
shape = x.shape
if valid_lens.dim() == 1:
valid_lens = torch.repeat_interleave(valid_lens, shape[1])
else:
valid_lens = valid_lens.reshape(-1)
x = sequence_mask(x.reshape(-1, shape[-1]), valid_lens, value=-1e6)
return torch.nn.functional.softmax(x.reshape(shape), dim=-1)为了说明此函数的工作原理,请考虑两个样本大小为 \(2 \times 4\) ,它们的有效长度是 2 和 3 ,经过掩码操作后,超过有效长度的地方都置为 0 :
print(masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3])))tensor([[[0.3590, 0.6410, 0.0000, 0.0000],
[0.4063, 0.5937, 0.0000, 0.0000]],
[[0.3408, 0.2334, 0.4258, 0.0000],
[0.2890, 0.3940, 0.3170, 0.0000]]])
同样,也可以使用二维张量,为矩阵样本中的每一行指定有效长度:
print(masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]])))tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
[0.3294, 0.4430, 0.2276, 0.0000]],
[[0.4534, 0.5466, 0.0000, 0.0000],
[0.1996, 0.3411, 0.2128, 0.2464]]])
9.1.5.2 缩放点积注意力
让我们回顾一下高斯核的注意力函数(没有指数部分):
首先,注意最后一项仅和 \(q\) 有关,对于所有的 \(q, k_i\) 数据对都是一样的。将注意力权重标准化,该项会完全消失。其次,批次归一化和层归一化都会导致激活具有良好界限,通常都是常数 \(\lVert k_i \rVert\) 。我们从 \(a\) 的定义中将 \(\lVert k_i \rVert\) 去掉,也不会对最终的输出造成大的影响。
最后我们需要控制参数的值,假定所有的查询 \(q \in R^d\) 和 键 \(k_i \in R^d\) 都是独立的,它们都是均值为 0 ,方差为 1 的随机变量。两个向量之间的点积均值为 0,方差为 \(d\) ,为了确保点积的方差仍然保持 1,无论向量的长度如何,我们使用 缩放点积注意力 (Scaled Dot-Product Attention) 评分函数。也就是说,我们将点积重新缩放为 \(\frac{1}{\sqrt{d}}\) 。因此得到了第一个常用的注意力函数:
注意力权重 \(\alpha\) 仍然需要归一化,利用 softmax 运算进一步简化这一个过程:
通常,缩放点积注意力要求查询和键具有相同的向量长度,例如 \(d\) ,尽管这个问题可以通过使用 \(q^\top Mk\) 代替 \(q^\top k\) 解决,其中 \(M\) 表示适合在两个空间进行平移的矩阵。
在实践中,我们通常从小批量的角度来考虑提高效率,例如基于 \(n\) 个查询和 \(m\) 个键-值对的计算,其中查询和键的长度为 \(d\) ,值的长度为 \(v\) 。查询 \(Q \in R^{n \times d}\) 、键 \(K \in R^{m \times d}\) 和值 \(V \in R^{m \times v}\) 的缩放点积注意力是:
下面就是具体的实现:
class DotProductAttention(nn.Module):
'''Scaled dot product attention.'''
def __init__(self, dropout):
super().__init__()
self.dropout = nn.Dropout(dropout)
# Shape of queries: (batch_size, no. of queries, d)
# Shape of keys: (batch_size, no. of key-value pairs, d)
# Shape of values: (batch_size, no. of key-value pairs, value dimension)
# Shape of valid_lens: (batch_size,) or (batch_size, no. of queries)
def forward(self, queries, keys, values, valid_lens=None):
d = queries.shape[-1]
# Swap the last two dimensions of keys with keys.transpose(1, 2).
scores = torch.bmm(queries, keys.transpose(1, 2)) / math.sqrt(d)
self.attention_weights = masked_softmax(scores, valid_lens)
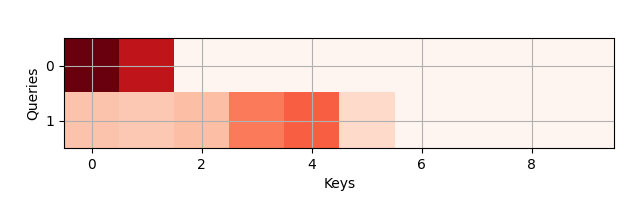
return torch.bmm(self.dropout(self.attention_weights), values)为了展示 DotProductAttention 类型是如何工作的,我们假设小批量的大小是 2 ,总共包括 10 个键值对,值的维度是 4 ,最后假设合法长度是 2 和 6 。那么我们的输出是一个 \(2 \times 1 \times 4 \) 的张量:
queries = torch.normal(0, 1, (2, 1, 2))
keys = torch.normal(0, 1, (2, 10, 2))
values = torch.normal(0, 1, (2, 10, 4))
valid_lens = torch.tensor([2, 6])
attention = DotProductAttention(dropout=0.1)
attention.eval()
assert attention(queries, keys, values, valid_lens).shape == (2, 1, 4)
show_heatmap(attention.attention_weights.reshape((1, 1, 2, 10)),
x_label='Keys', y_label='Queries')让我们检查一下注意力权重是否真的会在第二列和第六列之后消失(因为将有效长度设置为 2 和 6):
9.1.5.3 加性注意力
当查询 \(q\) 和键 \(k\) 是不同维度的矢量时,可以使用矩阵 \(q^\top Mk\) 来解决不匹配问题,或者使用 加性注意力 (Additive Attention) 作为评分函数。一个好处是,正如其名所示,注意力用的是加法,这可以节省一些资源。给定一个查询 \(q \in R^q\) 和键 \(k \in R^k\) ,加性注意力的评分函数为:
其中可学习参数 \(W_q \in R^{h \times q}\) 、\(W_k \in R^{h \times k}\) 和 \(w_v \in R^h\) 。然后将该项输入到 softmax 中,以确保非负性和正则化。加性注意力的一个等效解释是,将查询和键连接起来,并输入到具有单个隐藏层的 MLP 中,使用 tanh 作为激活函数和禁用偏置项,我们实现的加性注意力如下:
class AdditiveAttention(nn.Module):
'''Additive attention.'''
def __init__(self, num_hiddens, dropout, **kwargs):
super(AdditiveAttention, self).__init__(**kwargs)
self.W_k = nn.LazyLinear(num_hiddens, bias=False)
self.W_q = nn.LazyLinear(num_hiddens, bias=False)
self.w_v = nn.LazyLinear(1, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens):
queries, keys = self.W_q(queries), self.W_k(keys)
assert queries.shape == (2, 1, 8)
assert keys.shape == (2, 10, 8)
# After dimension expansion, shape of queries: (batch_size, no. of
# queries, 1, num_hiddens) and shape of keys: (batch_size, 1, no. of
# key-value pairs, num_hiddens). Sum them up with broadcasting
features = queries.unsqueeze(2) + keys.unsqueeze(1)
assert features.shape == (2, 1, 10, 8)
features = torch.tanh(features)
# There is only one output of self.w_v, so we remove the last
# one-dimensional entry from the shape. Shape of scores: (batch_size,
# no. of queries, no. of key-value pairs)
scores = self.w_v(features).squeeze(-1)
assert scores.shape == (2, 1, 10)
assert values.shape == (2, 10, 4)
self.attention_weights = masked_softmax(scores, valid_lens)
# Shape of values: (batch_size, no. of key-value pairs, value
# dimension)
return torch.bmm(self.dropout(self.attention_weights), values)让我们看看 AdditiveAttention 是如何工作的,设置查询、键与值的大小分别为 \((2, 1, 20)\) 、 \((2, 10, 2)\) 和 \((2, 10, 4)\) 。和 DotProductAttention 的选择相同,只是现在查询是 20 维。同样,选取 \((2, 6)\) 作为小批量中序列的有效长度。
# 2 个样本,每个样本 1 个查询向量,维度是 20
queries = torch.normal(0, 1, (2, 1, 20))
keys = torch.normal(0, 1, (2, 10, 2))
values = torch.normal(0, 1, (2, 10, 4))
valid_lens = torch.tensor([2, 6])
attention = AdditiveAttention(num_hiddens=8, dropout=0.1)
attention.eval()
assert attention(queries, keys, values, valid_lens).shape == (2, 1, 4)
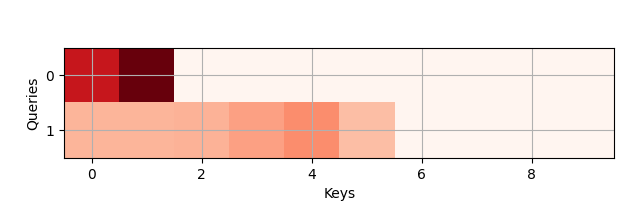
show_heatmap(attention.attention_weights.detach().reshape((1, 1, 2, 10)),
x_label='Keys', y_label='Queries')当查看热力图时,和 DotProductAttention 有非常类似的行为,只在选定的有效范围内的词是非零的:
9.1.6 Bahdanau 模型
当我们进行机器翻译时,Seq2Seq 模型使用两个 RNN 设计了一个编码器-解码器架构,用于处理序列到序列学习。具体来说,RNN 编码器将可变长度的序列转换为固定形状的上下文变量,然后 RNN 解码器根据生成的标记和上下文变量,逐个标记地生成输出(目标)序列。
通常在 RNN 中,所有关于源序列的相关信息都会被编码器转换为某种内部固定维度的状态表示。解码器正是使用这个状态作为生成翻译序列的完整且唯一的信息源。换句话说,序列到序列机制将中间状态市委任何可能作为输入的字符串的充分统计量。
虽然这对于短序列来说非常合理,但对于长序列(例如书中的一章或甚至是一个非常长的句子)显然是不可行的。毕竟,不久之后,中间表示中就没有足够的“空间”来存储源序列中所有重要的内容。因此,解码器将无法翻译长而复杂的句子。
第一个遇到这个问题的人之一是 Graves ,他尝试设计一个 RNN 来生成手写文本。由于源文本具有任意长度,他们设计了一个可微分的注意力模型来将文本字符与更长的笔迹对齐,其中对齐仅在一个方向上移动。反过来,这借鉴了语音识别中的解码算法,例如隐马尔可夫模型。
受学习对齐思想的启发, Bahdanau 等人(2014)提出了一种可微分注意力模型,摆脱了单向对齐的限制。在预测某个 token 时,如果并非所有输入 token 都相关,则该模型会仅对齐(或关注)输入序列中与当前预测相关的部分。之后,在生成下一个 token 之前,该模型会用它来更新当前状态。尽管Bahdanau 的这种注意力机制描述起来并无恶意,但它无疑已成为过去十年深度学习领域最具影响力的思想之一,并催生了 Transformer 以及许多相关的新架构。
9.1.6.1 模型架构
模型的关键思想是,我们不再保存状态,比如源句子的上下文变量 \(c\) 。会根据源句子(编码器的隐藏状态 \(h_t\))和已经生成的文本(解码器的隐藏状态\(s_{t'-1}\))来动态更新。生成的结果为 \(c_{t'}\) ,在时间步长 \(t'\) 之后就会被更新。假设输入序列的长度为 \(T\) ,那么经过注意力汇聚的上下文输出如下公式所示:
我们使用 \(s_{t'-1}\) 作为查询,\(h_t\) 既是键也是值。记住 \(c_{t'}\) 用于生成状态 \(s_{t'}\) ,进而产生新的标记。注意力权重 \(\alpha\) 使用加性注意力评分函数,Bahdanau 模型架构如下图所示:
9.1.6.2 带注意力的解码器
要实现带注意力机制的 RNN 编码器-解码器,我们只需重新定义解码器,全部实现在文件 bahdanau.py 中,我们需要在Seq2SeqAttentionDecoder 类中实现 RNN 解码器。解码器的状态使用以下参数初始化:(i) 所有时间步长中编码器最后一层的隐藏状态,用作注意力机制的键和值;(ii) 最后时间步长中编码器所有层的隐藏状态,用于初始化解码器的隐藏状态;以及 (iii) 编码器的有效长度,用于排除注意力池中的填充标记。在每个解码时间步长中,前一时间步长获得的解码器最后一层的隐藏状态用作注意力机制的查询。注意力机制的输出和输入嵌入被连接起来作为 RNN 解码器的输入。
class Seq2SeqAttentionDecoder(AttentionDecoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0):
super().__init__()
self.attention = AdditiveAttention(num_hiddens, dropout)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.GRU(
embed_size + num_hiddens, num_hiddens, num_layers,
dropout=dropout)
self.dense = nn.LazyLinear(vocab_size)
def init_state(self, enc_outputs, enc_valid_lens):
# Shape of outputs: (num_steps, batch_size, num_hiddens).
# Shape of hidden_state: (num_layers, batch_size, num_hiddens)
outputs, hidden_state = enc_outputs
return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)
def forward(self, X, state):
# Shape of enc_outputs: (batch_size, num_steps, num_hiddens).
# Shape of hidden_state: (num_layers, batch_size, num_hiddens)
enc_outputs, hidden_state, enc_valid_lens = state
# Shape of the output X: (num_steps, batch_size, embed_size)
X = self.embedding(X).permute(1, 0, 2)
outputs, self._attention_weights = [], []
for x in X:
# Shape of query: (batch_size, 1, num_hiddens)
query = torch.unsqueeze(hidden_state[-1], dim=1)
# Shape of context: (batch_size, 1, num_hiddens)
context = self.attention(
query, enc_outputs, enc_outputs, enc_valid_lens)
# Concatenate on the feature dimension
x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
# Reshape x as (1, batch_size, embed_size + num_hiddens)
out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
outputs.append(out)
self._attention_weights.append(self.attention.attention_weights)
# After fully connected layer transformation, shape of outputs:
# (num_steps, batch_size, vocab_size)
outputs = self.dense(torch.cat(outputs, dim=0))
return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,
enc_valid_lens]
@property
def attention_weights(self):
return self._attention_weights接下来,我们使用四个序列的小批量来测试已实现的解码器,每个序列有七个时间步长:
vocab_size, embed_size, num_hiddens, num_layers = 10, 8, 16, 2
batch_size, num_steps = 4, 7
encoder = Seq2SeqEncoder(vocab_size, embed_size, num_hiddens, num_layers)
decoder = Seq2SeqAttentionDecoder(vocab_size, embed_size, num_hiddens,
num_layers)
X = torch.zeros((batch_size, num_steps), dtype=torch.long)
state = decoder.init_state(encoder(X), None)
output, state = decoder(X, state)
assert output.shape == (batch_size, num_steps, vocab_size)
assert state[0].shape == (batch_size, num_steps, num_hiddens)
assert state[1][0].shape == (batch_size, num_hiddens)9.1.6.3 训练
现在我们指定了新的解码器,实例化常规编码器和带有注意力的解码器,并训练该模型进行机器翻译:
data = MTFraEng(batch_size=128)
embed_size, num_hiddens, num_layers, dropout = 256, 256, 2, 0.2
encoder = Seq2SeqEncoder(
len(data.src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqAttentionDecoder(
len(data.tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
epochs = 30
model = Seq2Seq(encoder, decoder, tgt_pad=data.tgt_vocab[''], lr=0.005)
trainer = Trainer(max_epochs=epochs, gradient_clip_val=1)
(train_his, val_his) = trainer.fit(model, data)
pyplot.plot(range(1, epochs + 1), train_his, label='Train Loss', color='blue', marker='o')
pyplot.plot(range(1, epochs + 1), val_his, label='Validation Loss', color='red', marker='o')
pyplot.legend()
pyplot.grid()
pyplot.show() 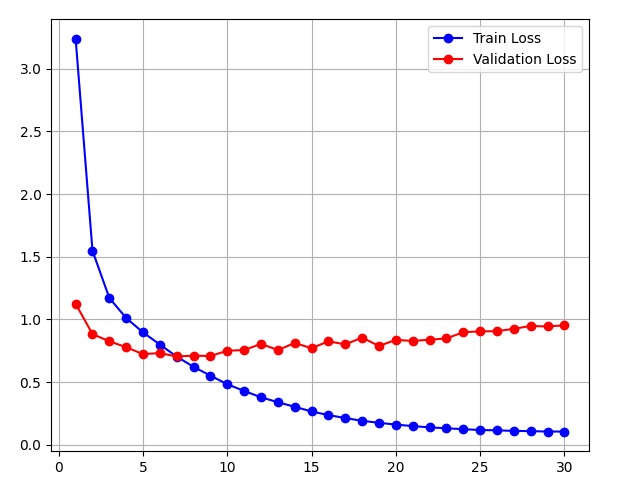
模型训练完成后,我们用它将一些英语句子翻译成法语并计算其 BLEU 分数:
engs = ['go .', 'i lost .', 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
preds, _ = model.predict_step(
data.build(engs, fras), data.num_steps)
for en, fr, p in zip(engs, fras, preds):
translation = []
for token in data.tgt_vocab.to_tokens(p):
if token == '':
break
translation.append(token)
print(f'{en} => {translation}, bleu,'
f'{bleu(" ".join(translation), fr, k=2):.3f}') go . => ['va', '!'], bleu,1.000 i lost . => ["j'ai", 'perdu', '.'], bleu,1.000 he's calm . => ['je', 'vais', 'bien', '.'], bleu,0.000 i'm home . => ['je', 'suis', 'chez', 'moi', '.'], bleu,1.000
让我们将翻译最后一句英文句子时的注意力权重可视化。我们可以看到,每个查询在键值对上分配的权重并不均匀。这表明,在每个解码步骤中,输入序列的不同部分都会被选择性地聚合到注意力池中:
_, dec_attention_weights = model.predict_step(
data.build([engs[-1]], [fras[-1]]), data.num_steps, True)
attention_weights = torch.cat([step[0][0][0] for step in dec_attention_weights], 0)
attention_weights = attention_weights.reshape((1, 1, -1, data.num_steps))
# Plus one to include the end-of-sequence token.
show_heatmap(attention_weights[:, :, :, :len(engs[-1].split()) + 1].detach().numpy(),
x_label='Key positions', y_label='Query positions')
在预测一个 token 时,如果并非所有输入 token 都相关,则采用 Bahdanau 注意力机制的 RNN 编码器-解码器会选择性地聚合输入序列的不同部分。这是通过将状态(上下文变量)视为加性注意力池的输出来实现的。在 RNN 编码器-解码器中,Bahdanau 注意力机制将前一时间步的解码器隐藏状态视为查询,并将所有时间步的编码器隐藏状态视为键和值。