Activation Function

2.4 Activation Function

Some common activation functions are summarized and their derivatives are solved.

Created Date: 2025-05-10

The activation function of a node in an artificial neural network is a function that calculates the output of the node based on its individual inputs and their weights.

2.4.1 Sigmoid Function

A sigmoid function is any mathematical function whose graph has a characteristic S-shaped or sigmoid curve.

A common example of a sigmoid function is the logistic function, which is defined by the formula:

\(\sigma(x) = \frac{1}{1 + e^{-x}} = \frac{e^x}{1 + e^x}\)

File sigmoid_demo.py defines a sigmoid function and its derivative, and plots the function and its derivative.

def sigmoid(x):
    return 1 / (1 + numpy.exp(-x))


def deriv_sigmoid(x):
    return sigmoid(x) * (1 - sigmoid(x))

x = numpy.linspace(-10, 10, 400)
pyplot.plot(x, sigmoid(x), label="f(x) = 1 / (1 + e^-x)")
pyplot.plot(x, deriv_sigmoid(x), label="f'(x) = f(x) * (1 - f(x))")
pyplot.legend()
pyplot.grid(True)
pyplot.subplots_adjust(left=0.08, right=0.92, top=0.96, bottom=0.06)
pyplot.show()

print("The derivative at x = 2 is", numpy.round(deriv_sigmoid(2), 4))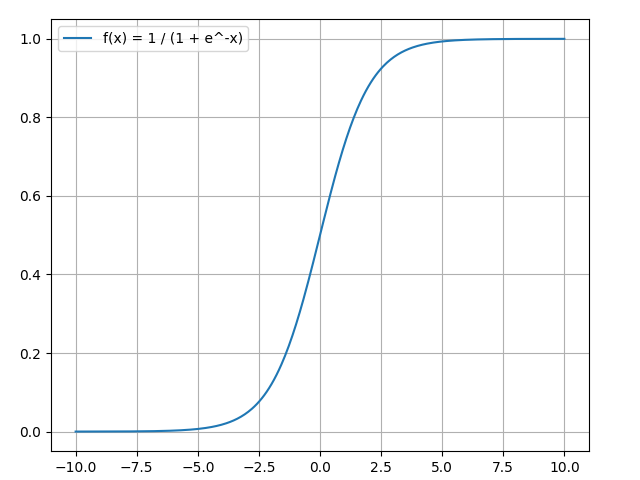

Figure 1 - Sigmoid Function

The derivative at x = 2 from scratch is 0.105

To compute the derivative of the sigmoid function using PyTorch, we can use the following code:

x_val = torch.tensor([2.0], requires_grad=True)
output = torch.sigmoid(x_val)
output.backward()
print("The derivative at x = 2 using PyTorch is", numpy.round(x_val.grad.item(), 4))

The derivative at x = 2 using PyTorch is 0.105

2.4.2 ReLU Function

One of the most popular and widely-used activation functions is ReLU (rectified linear unit). As with other activation functions, it provides non-linearity to the model for better computation performance.

The ReLU activation function has the form:

\(f(x) = max(0, x)\)

The ReLU function outputs the maximum between its input and zero, as shown by the graph. For positive inputs, the output of the function is equal to the input. For strictly negative inputs, the output of the function is equal to zero.

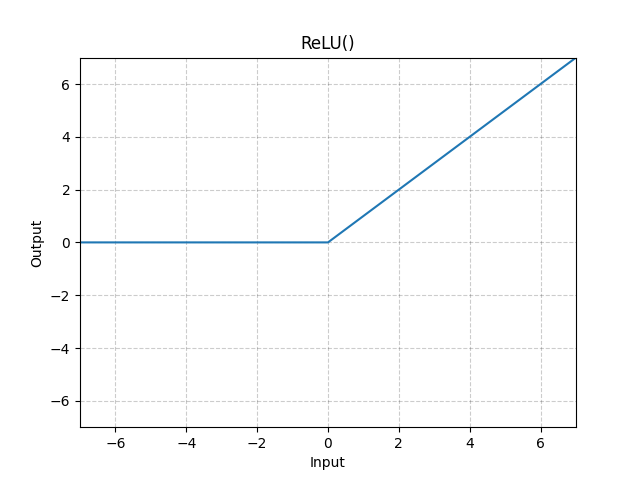
Figure 2 - ReLU Function

# To see the gradients, we need to enable gradient tracking and perform a backward pass.
input = torch.randn(10, requires_grad=True)
print("Input:", input)


def relu_scratch(input):
    # Custom implementation of ReLU activation function.
    return torch.maximum(torch.tensor(0.0), input)


output_scratch = relu_scratch(input)
print("Output after ReLU activation:", output_scratch)

Input: tensor([-1.7783,  1.1925, -0.1910, -0.7291, -1.3044, -0.1538,  1.3874,  2.5825,
         0.4784, -0.2474], requires_grad=True)
Output after ReLU activation: tensor([0.0000, 1.1925, 0.0000, 0.0000, 0.0000, 0.0000, 1.3874, 2.5825, 0.4784,
        0.0000], grad_fn=<MaximumBackward0>)

output_scratch = relu_scratch(input)
print("Output after ReLU activation:", output_scratch)

relu_torch = torch.nn.ReLU()
output = relu_torch(input)
print("Output after ReLU activation:", output)

Output after ReLU activation: tensor([0.0000, 1.1925, 0.0000, 0.0000, 0.0000, 0.0000, 1.3874, 2.5825, 0.4784,
        0.0000], grad_fn=<ReluBackward0>)

To compute the gradient of the ReLU function, we can use the following code:

gradients = torch.autograd.grad(outputs=output.sum(), inputs=input)[0]
print("Gradients:", gradients)

Gradients: tensor([0., 1., 0., 0., 0., 0., 1., 1., 1., 0.])

2.4.3 Tanh Function

2.4.4 Softmax Function

The softmax function is a mathematical function that transforms a vector of numbers into a probability distribution. It's commonly used in the output layer of neural networks for multi-class classification, ensuring that the outputs are between 0 and 1 and sum up to 1. This allows the outputs to be interpreted as probabilities for each class:

\(S(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}}\)

torch.nn.Softmax

2.4.5 Gaussian Error Linear Unit

The GELU (Gaussian Error Linear Unit) activation function is a smooth, differentiable alternative to the ReLU (Rectified Linear Unit) activation function, widely used in deep learning, particularly in transformer models like BERT. It addresses some of ReLU's limitations, such as the "dying ReLU" problem and its non-differentiability at zero.

The GELU function is defined as:

\(GELU(x) = x \times \Phi(x)\)

where \Phi(x) is the cumulative distribution function of the standard normal distribution.